Prism is a solid shape with two of its faces as parallel and identical polygons and the rest of the faces connecting them being parallelograms. In this article, we are going to discuss various prism formulas, different types of prisms and more.
There are mainly two types of prisms: right prisms and oblique prisms. The main difference between right and oblique prisms is that the lateral sides of a right prism are rectangles and not parallelograms.
Prisms are used in many fields in the world, but their biggest application is in the bending of light rays.

Index
History
Prism was first mentioned in one of Euclid’s mathematical treatises, the Elements. In the book he defined a prism as “a solid figure contained by two opposite, equal and parallel planes, while the rest are parallelograms”. The statements that followed included prisms in them and had examples of triangular-based prisms, this confused the geometricians that came later.

The Prism Formula
A prism, like all solids, has some common physical quantities, like volume and surface area. These quantities are important, as prisms are mainly used in optical or light related instruments precision in their dimensions is very important.
Some of the basic physical measurements of a prism are its surface area and volume.
Surface Area of Prism Formula
The surface area of any solid object is the region covered by its outer surface. The surface area of prism formula is calculated using the following general formula.
\(\text{Surface Area of a Prism} = 2(\text{Area of Base Polygons}) + \text{Lateral Surface Area}\)By substituting the values of area of the base and lateral surface area of a prism in the above formula, we can find its total surface area.
Let us consider the example of a triangular prism and find its surface area using above formula.
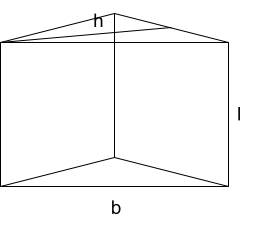
\(\text{Surface Area} = 2 \times (\frac{1}{2})(b)(h) + (3)(b)(l)\)
Volume of Prism Formula
The volume of a solid object is the amount of air it encloses inside its surfaces. The volume of prism formula can be calculated using the following equation.
\(\text{Volume of a Prism} = (\text{Area of the Base Polygon}) (\text{Height of the Prism})\)
\(\text{Volume} = \frac{1}{2} \times A \times h\)
Let us take the example of a triangular prism and calculate its volume using the above formula.

\(\text{Volume} = (\frac{1}{2})(b)(h)(l)\)
Types of Prisms
There are various types of prism having different formula which are named using different factors. We have discussed some of the factors down here.
Based on Shape of Bases
Prisms are named after their base polygon. There are many different types of prisms, but some of the most commonly used ones are triangular prism, rectangular prism, pentagonal prism and hexagonal prism. All the types of prisms mentioned here are right prisms.
Prisms which have an irregular polygon as their base are classified as irregular prisms.
Based on Angle Between Joining and Base
Right Prism: If all edges connecting the bases of the prism are perpendicular to the bases then the prism is called a right prism.
Oblique Prism: If edges connecting the bases and the bases are not perpendicular then the prism is called an oblique prism.
Applications of Prism
- Right-angled prisms can be used to make beam-splitter cubes.

- Right-angled prisms can also be used to rotate images by 90o or 180o. The orientation of the prism determines the angle and direction inversion.
- A combination of prisms called the porro system is used in binocular and telescope like instruments. This is used because it can rotate an image by 180o and still preserve its orientation(right-left handed).
- Hexagonal prisms are used in architecture. Triangular prisms structures are used in Sweden architecture to prevent snow from piling up on rooftops.
Example Problems on Prism Formula
Problem. A prism has a volume of 27 cm3, and a height of 9 cm. Then find the dimensions of base polygon if:
- The prism is a triangular prism
- The prism is a hexagonal prism
Solution. Given that,
The volume of prism = V = 27 cm3
The height of prism = H = 9 cm
We know that, volume of prism formula is given as,
\(\text{Volume of Prism} = (\text{Base Area}) (\text{Height})\)
\(\text{Base Area} = \frac{\text{Volume of prism}}{\text{height}}\)
\(\text{Base Area} = \frac{27}{9} = 3 \, cm^2\)
Therefore, the base area of any prism must be 3 cm2.
1. Considering Triangular Prism:
Here, the base polygon is a triangle. So,
\(\text{Base Area} = \frac{1}{2}bh\)
Since, the base triangle is equilateral,
\(\text{Base Area} = \frac{\sqrt{3}}{2}a^2\)
\(\frac{\sqrt{3}}{2}a^2 = 3\)
\(a^2 = 2 \sqrt{3}\)
\(a =1.86121 \, cm\)
Therefore, the side length of the base triangle is 1.86121 cm.
2. Considering Hexagonal Prism
Here the base polygon is a regular hexagon. So,
\(\text{Base Area} = 3 \sqrt{3}a^2\)
\(3 \sqrt{3}a^2 = 3\)
\(a^2 = \frac{1}{\sqrt{3}}\)
\(a = 0.75984 \, cm\)
Therefore, the side length of the base hexagon is 0.75984 cm.
FAQs
A prism is a 3-dimensional solid with two sides as regular polygons and the others as parallelograms.
There are two different types of prisms based on the angle between the base polygon and the side parallelograms:
1. Right prisms
2. Oblique prisms
Prisms can also be categorized based on the polygon at their base. Different prisms are named after the polygons at their bases, like triangular prism, rectangular prism, pentagonal prism, hexagonal prism, etc.
For a solid to become a prism, two of its opposite faces must be congruent polygons which are parallel to each other, and all the other faces connect them must be parallelograms.
The prism formula are used for calculating area, volume and other such quantities, or to find the dimensions of the prism using their area and volume.
Related Articles: