A dihedral angle is basically an angle made by two intersecting cartesian planes. Usually, we see angles between two lines but there are a lot of cases wherein we have intersecting planes and therefore angles between planes. So, let us dig more into this dihedral angle.
Index
Dihedral Angle Explained
Two planes can directly or indirectly intersect each other. The angle formed by the two planes is called the dihedral angle.
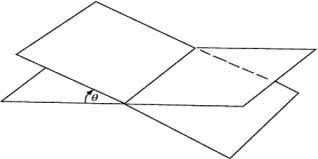
Let us name the two planes in the above figure as \(P\) and \(Q\).
As we can see the dihedral angle in the above figure is \(\theta\).
Properties of Dihedral Angle
The properties of intersecting angle between two planes are discussed below.
- In the above figure, it can be observed that apart from the angle \(\theta\), another angle can be formed on the right side, which is obtuse. The dihedral angle generally refers to the acute angle.
- The dihedral angles between two parallel planes is 0°, as they never intersect.
- It can be found to be the interior angle in any 3D shape as well.
Dihedral Angle Formula
Consider the above two intersecting planes, \(P\) and \(Q\). The equations of the two planes are,
\(a_1x + b_1y + c_1z + d_1 = 0\)
\(a_2x + b_2y + c_2z + d_2 = 0\)
Let the normal vectors to each plane be denoted as \(\overrightarrow{n_1}\) and \(\overrightarrow{n_2}\). Then,
\(\overrightarrow{n_1} = (a_1, b_1, c_1)\) and \(\overrightarrow{n_2} = (a_2, b_2, c_2)\)
We thus have,
\(\cos \theta = \frac{\overrightarrow{n_1} . \overrightarrow{n_2}}{\overrightarrow{n_1} \overrightarrow{n_2}}\)
where, \(\overrightarrow{n_1} . \overrightarrow{n_2}\) is the dot product of \(\overrightarrow{n_1}\) and \(\overrightarrow{n_2}\).
\(∴ \cos \theta = \frac{|a_1 a_2 + b_1 b_2 + c_1 c_2|}{\sqrt{a_1^2 + b_1^2 + c_1^2} \sqrt{a_2^2 + b_2^2 + c_2^2}}\)
Solved Examples
Question 1. Calculate the angle between planes \(x + 3y + z = 0\) and \(3x + y + 4z = 0\).
Solution. Given, \(x + 3y + z = 0\) and \(3x + y + 4z = 0\) are the equations of two planes.
The angle between the planes- \(\theta\) can be calculated from,
\(\begin{align}
\cos \theta & = \frac{|a_1 a_2 + b_1 b_2 + c_1 c_2|}{\sqrt{a_1^2 + b_1^2 + c_1^2} \sqrt{a_2^2 + b_2^2 + c_2^2}}\\
& = \frac{|1✕3 + 3✕1 + 1✕4|}{\sqrt{1^2 + 3^2 + 1^2} \sqrt{3^2 + 1^2 + 4^2}}\\
& = \frac{10}{\sqrt{286}} \approx 0.6504\\
\end{align}
\)
\(⇒ \cos \theta = \cos^{-1}(0.6504)\)
\(∴ \theta \approx 49.43°\)
Question 2. Two planes with the equation \(x + 7y – 3z + 8 = 0\) and \(3x – 2y + 4z – 1 = 0\) are given. Find the angle between them.
Solution. Given, \(x + 7y – 3z + 8 = 0\) and \(3x – 2y + 4z – 1 = 0\) are the equations of two planes.
The angle between the planes-\(\theta\) can be calculated from,
\(\cos \theta = \frac{|1✕3 + 7✕(-2) + (-3)✕4|}{\sqrt{1^2 + 7^2 + (-3)^2} \sqrt{3^2 + (-2)^2 + 4^2}}\)
\(⇒ \cos \theta = \frac{|-23|}{\sqrt{59}\sqrt{19}} = \frac{23}{\sqrt{1121}}\approx 0.68695\)
\(⇒ \cos \theta = \cos^{-1}(0.68695)\)
\(∴ \theta \approx 46.61°\)
FAQs
It is basically the acute angle between two planes and can be found using its formula given the equations of the planes.
In chemistry, it is the angle between two planes, which pass through the same bond. Specifically, it is the clockwise angle between half-planes through two sets of three atoms, having two atoms in common.
The formula is given as,
\(\cos \theta = \frac{|a_1 a_2 + b_1 b_2 + c_1 c_2|}{\sqrt{a_1^2 + b_1^2 + c_1^2} \sqrt{a_2^2 + b_2^2 + c_2^2}}\)
