Function rules are an essential part of mathematics that provide a way to model the relationship between variables. A function rule takes an input value and assigns to it exactly one output value, mapping inputs to outputs in a unique and predictable manner.
In this way, function rules provide a powerful tool for modelling real-world scenarios and solving mathematical problems.
The concept of function rules is fundamental to many branches of mathematics, including algebra, calculus, and statistics. By defining the relationship between variables, function rules allow us to make predictions, draw conclusions, and understand complex systems.
In this article, we will explore the characteristics of function rules, the different types of functions, how to determine if a given equation represents a function, and their real-world applications. Whether you are a student of mathematics or just curious about the subject, this article will provide an in-depth look at the fascinating world of function rules.
Index
Characteristics of a Function Rule
A function rule has several key characteristics that set it apart from other mathematical expressions:
A. Deterministic Property: One of the key characteristics of a function is that it is deterministic, meaning that given the same input, it will always produce the same output. This property makes functions ideal for modelling real-world scenarios where the relationship between two variables is well-defined.
B. Input and Output Values: A function takes an input value and assigns to it exactly one output value. The input values are commonly referred to as the independent variable, while the output values are known as the dependent variable. The function rule defines the relationship between these two variables.
C. Representation as Mathematical Equation: Function rules are often represented by mathematical equations, such as y = 2x + 1. These equations provide a compact and easily understood representation of the relationship between the input and output values.
Types of Function Rules
Function rules come in many different forms, each with its own unique characteristics and applications. Some of the most common types of function rules include:
Linear Functions
Linear functions are those where the relationship between the independent and dependent variables is a straight line.
These functions have the form y = mx + b,
where
m is the slope of the line and
b is the y-intercept.
Linear functions are widely used in a variety of applications, from modelling real-world scenarios to solving optimization problems.
Quadratic Functions
Quadratic functions are those where the relationship between the variables is a parabolic shape.
These functions have the form y = ax2 + bx + c,
where a, b, and c are constants.
Quadratic functions are commonly used in applications involving projectiles, parabolic reflectors, and optimization problems.
Exponential Functions
Exponential functions are those where the dependent variable is the power of the independent variable.
These functions have the form y = ax, where a is a constant and x is the independent variable.
Exponential functions are widely used in applications involving exponential growth and decay, such as population growth and radioactive decay.
Other Types of Functions
In addition to linear, quadratic, and exponential functions, there are many other types of functions, including 1. Logarithmic
2. Trigonometric
3. Polynomial functions, to name a few.
Each type of function has its own unique characteristics and applications, and understanding the different types of functions is an important part of a comprehensive mathematical education.
Testing for Functionality
Before using an equation as a function rule, it is important to verify that it meets the criteria for being a function. There are several methods for testing if an equation represents a function, including:
The Vertical Line Test
This test involves plotting the equation on a coordinate plane and checking if any vertical line intersects the graph at more than one point.
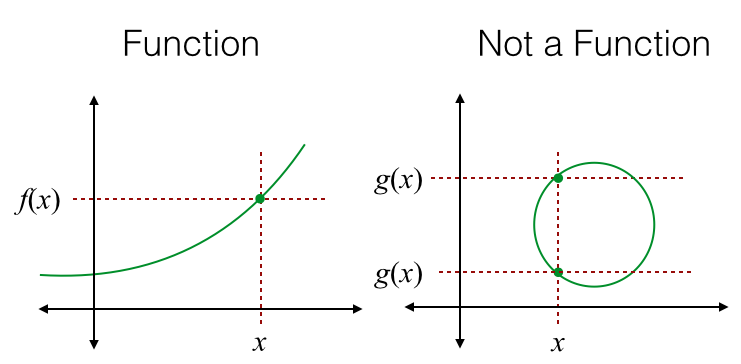
If it intersects at more than one place, the equation does not represent a function because it violates the deterministic property, as the same input value maps to multiple output values.
The Input-Output Test
This test involves listing several input values and their corresponding output values. If every input value map to exactly one output value, then the equation represents a function.
By using these tests, we can determine if an equation represents a function and use it as a tool for modelling real-world scenarios or solving mathematical problems.
Applications of Function Rules
Function rules have numerous real-world applications, providing a powerful tool for modelling and understanding the relationship between variables. Some of the most important applications of function rules include:
A. Modelling Physical Processes: Functions can be used to model a variety of physical processes, from the simple motion of an object under constant acceleration to more complex scenarios involving multiple variables. By using function rules, we can gain a deeper understanding of the underlying physical processes and make predictions about their behaviour.
B. Data Analysis: Function rules can be used to fit models to data sets, providing a powerful tool for data analysis. Whether it’s linear regression to fit a line to data or more complex models involving multiple variables, function rules provide a way to make sense of complex data sets and make predictions based on them.
C. Optimization: Function rules can be used to solve optimization problems, such as finding the maximum or minimum value of a function. These types of problems are commonly encountered in a variety of fields, including engineering, economics, and finance.
D. Mathematics and Physics: Function rules play a fundamental role in many areas of mathematics and physics, providing a way to model real-world scenarios and make predictions about their behaviour. From simple harmonic motion to complex physical processes involving multiple variables, function rules provide a powerful tool for understanding the world around us.
Conclusion
In conclusion, function rules are a fundamental mathematical concept that provide a way to model the relationship between variables. Whether it’s a simple linear relationship or a complex relationship involving multiple variables, function rules provide a powerful tool for understanding the world around us. Understanding the different types of function rules, how to test for functionality, and the many applications of function rules is an important part of a comprehensive mathematical education.
