Coincident lines are an important concept in analytical geometry and algebra, such as linear equations. They have some interesting properties discussed below.
In non-mathematical terms, these lines are simply those which lie on top of each other.
Mathematically, these lines are those which share all their points and can be represented by the same equation.
Index
How Do Coincident Lines Look?
When graphed, coincident lines lie on top of each other, so they look like one line. They cannot be distinguished by looking at all.
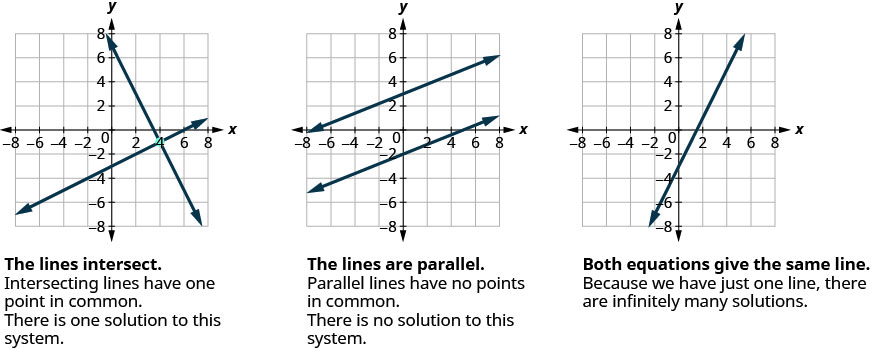
Identification from Equations
In this section, we will see how to identify coincident line, based on their equations.
Slope-Intercept Form
Consider a pair of lines, with slope-intercept equations as follows:
\(y = m_1 x + c_1\)
\(y = m_2 x + c_2\)
These lines are coincident if and only if:
\(m_1 = m_2 \textbf{ and } c_1 = c_2\)
i.e their slopes and intercepts should be equal.
Standard Form
Consider two lines in standard form, as follows:
\(A_1x + B_1y + C_1 = 0\)
\(A_2x + B_2y + C_2 = 0\)
In this case, the lines are coincident if and only if:
\(\frac{A_1}{A_2} = \frac{B_1}{B_2} = \frac{C_1}{C_2}\)
This condition can also be called the coincident line’s formula.
Difference Between Coincident Lines and Parallel Lines
These two are very similar concepts. In fact, coincident lines are a special case of parallel lines. However, there are a few differences.
When graphed, parallel lines look like two separate lines, visually and never intersect. Whereas, Coincident lines cannot be visually separated the same way and they intersect at all of its points.
Applications
These special types of lines occur in algebra, for example in simultaneous equations. They correspond to a special case, and it means that they have infinite solutions in common.
For example, consider the two equations,
\(2y – 3x = 4\) and,
\(4y – 6x =8\)
The pair of values, \(x = 5\) and \(y = 2\) satisfy the first equation. Substituting this in the second equation, the LHS gives \(4(5) – 6(2) = 20-12 = 8\) which is the RHS. So \(x = 5\) and \(y = 2\) also satisfies the second equation. This applies to any pair of \((x, y)\) values that satisfies any one of the equations.
Solved Examples
Question 1. Are the lines given by equations \(3x + 4y = 10\) and \(6x + 8y = 20\) coincident?
Solution. We first write the lines in standard form, as follows:
\(3x + 4y -10 = 0\)
\(6x + 8y -20 = 0\)
For the first equation, we have:
\(A_1 = 3 ; B_1 = 4 ; C_1 = -10\)
For the second equation, we have:
\(A_1 = 6 ; B_1 = 8 ; C_1 = -20\)
Now we calculate \(\frac{A_1}{A_2}\), \(\frac{B_1}{B_2}\) and \(\frac{C_1}{C_2}\)
\(\frac{A_1}{A_2} = \frac{3}{6} = 0.5\)
\(\frac{B_1}{B_2} = \frac{4}{8} = 0.5\)
\(\frac{C_1}{C_2} = \frac{-10}{-20} = 0.5\)
Thus, this satisfies the condition:
\(\frac{A_1}{A_2} = \frac{B_1}{B_2} = \frac{C_1}{C_2}\)
The given pair is coincident.
Question 2. What must be the value of \(k\) for the two given lines to be coincident?
\(2x – 4y = 6\) and \(2y – x = k\).
Solution. We again write these equations in standard form.
\(2x – 4y – 6 = 0\)
\(-x + 2y -k =0\)
We have, for the first equation,
\(A_1 = 2 ; B_1 = -4 ; C_1 = -6\)
And, for second equation,
\(A_1 = -1 ; B_1 = 2 ; C_1 = -k\)
For the lines to coincide, the following requirement must be satisfied:
\(\frac{A_1}{A_2} = \frac{B_1}{B_2} = \frac{C_1}{C_2}\)
So, we calculate each of them.
\(\frac{A_1}{A_2} = \frac{2}{-1} = -2\)
\(\frac{B_1}{B_2} = \frac{-4}{2} = -2\)
\(\frac{C_1}{C_2} = \frac{-6}{-k}\)
Assuming they are coincident, \(\frac{-6}{-k} = -2\).
Solving for \(k\), we get, \(k = -3\).
FAQs
They are simply lines that lie on top of each other.
Two lines are coincident if their slopes and intercepts are equal.
Yes, they do intersect. In fact, they intersect at all points they have, which are in common.
These lines share all their points i.e intersect at all the points, so, all the points are solutions. As a line have infinite points, there exist infinite solutions for these types of lines.
