String waves are an example of transverse waves. A transverse wave is a wave whose oscillations are perpendicular to the direction of the wave’s propagation. In this article, we will see some important string waves formulas which will also help you in preparation for competitive exams like JEE and NEET.
GENERAL EQUATION OF WAVE MOTION:
\( \frac{\partial ^{2}y}{\partial t^{2}}=v^{2}\frac{\partial ^{2}y}{\partial x^{2}} \) \( y\left ( x,t \right )=f\left ( t\pm \frac{x}{v} \right ) \)where, y (x, t) should be finite everywhere.
\( \Rightarrow \) \( f\left ( t+\frac{x}{v} \right ) \) represents wave travelling in – ve x-axis.
\( \Rightarrow \) \( f\left ( t-\frac{x}{v} \right ) \) represents wave travelling in + ve x-axis.
y = A sin \( \left ( \omega t\pm kx+\phi \right ) \)
TERMS RELATED TO WAVE MOTION ( FOR 1-D PROGRESSIVESINE WAVE)
Wave number (or propagation constant) (k): \(k=\frac{2\pi }{\lambda }=\frac{\omega }{v} \) (rad m–1)
Phase of wave : The argument of harmonic function \( \left ( \omega t\pm kx+\phi \right ) \) is called phase of the wave.
Phase difference \( \left ( \Delta \phi \right ) \) : difference in phases of two particles at any
time t.
\( \Delta \phi=\frac{2\pi }{\lambda }\Delta x \) Also. \( \Delta \phi=\frac{2\pi }{T }\cdot \Delta t \)
SPEED OF TRANSVERSE WAVE ALONG A STRING/WIRE.
\( v=\sqrt{\frac{T}{\mu }} \) where \( \begin{align} T &=Tension \ \\\mu &=mass\;per\;unit\;length \end{align}\)
POWER TRANSMITTED ALONG THE STRING BY A SINE WAVE
Average Power \( \left \langle p \right \rangle=2\pi ^{2}f^{2}A^{2}\mu v \)
Intensity \( I=\frac{\left \langle P \right \rangle}{s}=2\pi ^{2}f^{2}A^{2}\rho v \)
REFLECTION AND REFRACTION OF WAVES
\( y_{i}=A_{1}sin\left ( \omega t-k_{1}x \right ) \)\( \begin{align} y_{t} &=A_{t}sin\left ( \omega t-k_{2}x \right ) \ \\y_{r} &=-A_{r}sin \left ( \omega t+k_{1}x \right ) \end{align} \)} if incident from rarer to denser medium \( \left ( v_{2}< v_{1} \right ) \)
\( \begin{align} y_{t} &=A_{t}sin\left ( \omega t-k_{2}x \right ) \ \\y_{r} &=-A_{r}sin \left ( \omega t+k_{1}x \right ) \end{align} \)} if incident from denser to rarer medium. \( \left ( v_{2}> v_{1} \right ) \)
Amplitude of reflected & transmitted waves
\( A_{r}=\frac{\left | k_{1}-k_{2} \right |}{k_{1}+k_{2}}A_{i} \) & \( A_{t}=\frac{2k_{1}}{k_{1}+k_{2}}A_{i} \)
STANDING/STATIONARY WAVES
\( y_{1}=Asin\left ( \omega t-kx+\Theta _{1} \right )\)
\( y_{2}=Asin\left ( \omega t+kx+\Theta _{2} \right ) \)
\( \Rightarrow \) \( y_{1}+y_{2}=\left [ 2Acos\left ( kx+\frac{\Theta {2}-\Theta {1}}{2} \right ) \right ]sin\left ( \omega t+\frac{\Theta {1}+\Theta {2}}{2} \right ) \)
The quantity \( 2A \cos\left ( kx+\frac{\Theta {2}-\Theta {1}}{2} \right ) \) represents resultant amplitude at x. At some position resultant amplitude is zero these are called nodes. At some positions resultant amplitude is 2A, these are called antinodes.
- Distance between successive nodes or antinodes \( =\frac{\lambda }{2} \)
- Distance between successive nodes and antinodes \( =\frac{\lambda }{4} \)
- All the particles in the same segment (portion between two successive nodes) vibrate in the same phase.
- The particles in two consecutive segments vibrate in the opposite phase.
- Since nodes are permanently at rest so energy can not be transmitted across them.
VIBRATIONS OF STRINGS ( STANDING WAVE)
(a) Fixed at both ends:
Fixed ends will be nodes. So waves for which
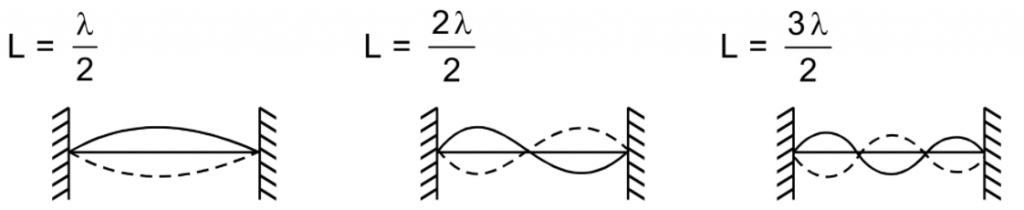
are possible giving
\( L=\frac{n\lambda }{2} \) or \( \lambda =\frac{2L }{n} \) where n = 1, 2, 3, ….
as \( v=\sqrt{\frac{T}{\mu }} \) \( f_{n}=\frac{n}{2L}\sqrt{\frac{T}{\mu }} \), n = no. of loops
(b) String free at one end:
For fundamental mode L \( =\frac{\lambda }{4} \) = or \( \lambda =4L \)

First overtone \( L=\frac{3\lambda }{4} \) Hence \( \lambda =\frac{4L }{3} \)

so \( f_{1}=\frac{3}{4L}\sqrt{\frac{T}{\mu }} \) (First overtone)
Second overtone \( f_{2}=\frac{5}{4L}\sqrt{\frac{T}{\mu }} \)
so \( f_{n}=\frac{\left ( n+\frac{1}{2} \right )}{2L}\sqrt{\frac{T}{\mu }} \) \( =\frac{\left ( 2n+1 \right )}{4L}\sqrt{\frac{T}{\mu }} \)
