Simple Harmonic Motion or SHM is a periodic motion where the restoring force is directly proportional to the magnitude of the object’s displacement and acts toward the object’s equilibrium position. In this article, we will see some important simple harmonic motion formulas which will also help you in preparation for competitive exams like JEE and NEET.
General equation of S.H.M. is x = A sin \( \left ( \omega t+\phi \right );\left ( \omega t+\phi \right ) \) is phase of the motion and \( \phi \) is initial phase of the motion.
Angular Frequency \( \left ( \omega \right ): \) \( \omega=\frac{2\pi }{T}=2\pi f \)
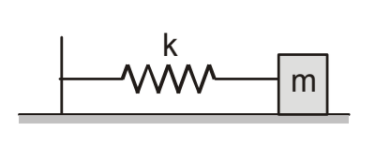
Time period (T) : \( T=\frac{2\pi }{\omega }=2\pi \sqrt{\frac{m}{k}} \)
Speed : \( v=\omega \sqrt{A^{2}-x^{2}} \)
Acceleration: \( a=-\omega ^{2}x \)
Kinetic Energy (KE) : \( \frac{1}{2}mv^{2}=\frac{1}{2}m\omega ^{2}\left ( A^{2}-x^{2} \right )=\frac{1}{2}k\left ( A^{2}-x^{2} \right ) \)
Potential Energy (PE) : \( \frac{1}{2}Kx^{2} \)
Total Mechanical Energy (TME)
\( =K.E.+P.E.=\frac{1}{2}k\left ( A^{2}-x^{2} \right )+\frac{1}{2}Kx^{2}=\frac{1}{2}KA^{2} \) (which is constant)
SPRING-MASS SYSTEM
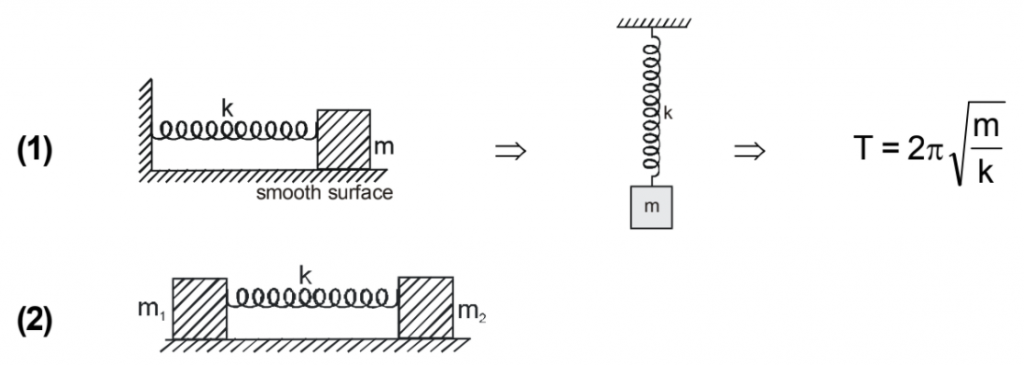
\( T=2\pi \sqrt{\frac{\mu }{K}} \) ,where \( \mu =\frac{m_{1}m_{2}}{\left ( m_{1}+m_{2} \right )} \) known as reduced mass
COMBINATION OF SPRINGS
Series Combination : \( 1/k_{eq}=1/k_{1}+1/k_{2} \)
Parallel combination : \( k_{eq}=k_{1}+k_{2} \)
SIMPLE PENDULUM \( T=2\pi \sqrt{\frac{\mathit{e}}{g}}=2\pi \sqrt{\frac{e}{g_{eff.}}} \) (in accelerating Reference Frame); \( g_{eff} \) is net acceleration due to pseudo force and gravitational force.
COMPOUND PENDULUM / PHYSICAL PENDULUM
Time period (T) : \( T=2\pi \sqrt{\frac{1}{mge}} \)
where, \( I=I_{cm}+ml^{2}\); \(l\) is distance between point of suspension and centre of mass
TORSIONAL PENDULUM
Time period (T) : \( T=2\pi \sqrt{\frac{1}{C}} \) where, C = Torsional constant
Superposition of SHM’s along the same direction \( x_{1}=A_{1}sin\omega t \) & \( x_{2}=A_{2}sin\left (\omega t+0 \right ) \)
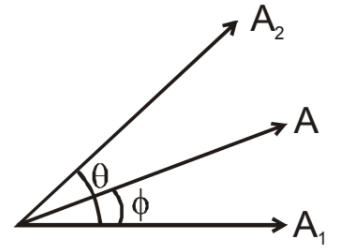
If equation of resultant SHM is taken as \( x=Asin\left ( \omega t+\phi \right ) \)
\( A=\sqrt{A_{1}^{2}+A_{2}^{2}+2A_{1}A_{2}cos\Theta} \) & \( tan\phi =\frac{A_{2}sin\Theta }{A_{1}+A_{2}cos\Theta } \)
1. Damped Oscillation
- Damping force \( \overrightarrow{F}=-b\overrightarrow{v} \)
- equation of motion is \( \frac{mdv}{dt}=-kx-bv \)
- \( b^{2}-4mK> 0 \) over damping
- \( b^{2}-4mK= 0 \) critical damping
- \( b^{2}-4mK< 0 \) under damping
- For small damping the solution is of the form. \( x=\left ( A_{0}e^{-bt/2m} \right )sin\left [ \omega ^{1}t+\delta \right ] \) , where \( \omega ‘=\sqrt{\left ( \frac{k}{m} \right )-\left ( \frac{b}{2m} \right )^{2}} \) For small b
- angular frequency \( \omega ‘\approx \sqrt{k/m,}=\omega _{0} \)
- Amplitude \( A=A_{o}e^{\frac{-bt}{2m}} \)
- Energy \( E\left ( t \right )=\frac{1}{2}KA^{2}e^{-bt/m} \)
- Quality factor or Q value , \( Q=2\pi \frac{E}{\left | \Delta E \right |}=\frac{\omega ‘}{2\omega _{y}} \) where , \( \omega ‘=\sqrt{\frac{k}{m}\cdot \frac{b^{2}}{4m^{2}}} \) , \( \omega _{y}=\frac{b}{2m} \)
2. Forced Oscillations And Resonance
External Force F(t) \( =F_{0} cos \omega_{d}t \) \( x\left ( t \right )=Acos\left ( \omega _{d}t+\phi \right ) \)
\( A=\frac{F_{0}}{\sqrt{\left ( m^{2}\left ( \omega ^{2}-\omega {d}^{2} \right )^{2}+\omega {d}^{2}b^{2} \right )}} \) and \( tan\phi =\frac{-v_{0}}{\omega {d}x{0}} \)
(a) Small Damping \( A=\frac{F_{0}}{m\left ( \omega ^{3}-\omega _{d}^{2} \right )} \)
(b) Driving Frequency Close to Natural Frequency \( A=\frac{F_{0}}{\omega _{d}b} \)
