Stokes Law

Stokes Law gives the relation between the velocity and frictional force acting on a spherical body moving in a viscous fluid. This law also gives the settling or terminal velocities of spherical objects moving in a viscous fluid column.

History

Stokes law was formulated by George Gabriel Stokes, an Irish born mathematical physicist. Stokes published his papers on fluid motion and friction of fluids even before he became the “Lucasian Professor of Mathematics” at Cambridge University in 1849. 

It is also interesting to note that despite being a scientist Stokes was a very religious person, highly interested in the links between science and faith.

The Law

The law states that the frictional force – or drag force – experienced by a solid spherical body moving in a viscous fluid is directly proportional to its velocity, radius and also the viscosity of the fluid. 

The equation of drag force or viscous force is,

\(
F_d = 6\pi\eta rv\\
\begin{array}{ll}
\mbox{here,} & F_d\mbox{ – is drag force}\\
& \eta\mbox{ – is viscosity of the fluid}\\
& r\mbox{ – is radius of the spherical solid object}\\
& v\mbox{ – is velocity of the solid object}\\
\end{array}
\)

This equation is also known as the Stokes Law equation. 

Stokes’ law makes the following assumptions for the behaviour of a particle in a fluid:
1. Laminar flow
2. Spherical particles
3. Homogeneous (uniform in composition) material
4. Smooth surfaces
5. Particles do not interfere with each other.

Proof

Here we will be proving stokes law using basic concepts of physics.

We know that drag force is proportional to velocity and radius of the object and also to the viscosity of the fluid.

So, \(F_d \propto \eta^a v^b r^c\)

=> \(F_d = K \eta^a v^b r^c\); here, K is proportionality constant

By using the concept of units,

=> \([MLT^{-2}] = [ML^{-1}T^{-1}]^{a} [LT^{-1}]^{b} [L]^{c}\)                         

By expanding LHS and simplifying we get,

=> \([MLT^{-2}] = M^{a}.L^{-a+b+c}.T^{-a-c}\)  

Now comparing LHS and RHS we get,

\(
a = 1 …(1)\\
-a + b + c = 1 …(2)\\
a + c = 2 …(3)\\
\mbox{Substituting (1) in (3) we get,}\\
c = 1 …(4)\\
\mbox{Using (1) and (4) in equation (2)}\\
b = 1
\)

Then by substituting the obtained values of a, b and c in the original relation of drag force we get,

\(F_d = K \eta v r\)

But the proportionality constant ‘K’ was not derived but experimentally obtained by stokes as 6π.

Hence, the equation of stokes law becomes \(F_d = 6\pi\eta rv\). This equation is commonly known as the Stokes Law formula.

Terminal velocity

When a spherical object freely falls under gravity in a long liquid column, its velocity becomes constant after a certain period of time. This constant velocity is called Terminal Velocity.

Let us consider a spherical object of radius ‘r’ is falling under gravity in a long liquid column where ‘\(\eta\)’ is the viscosity of the liquid. The object obtains a terminal velocity say ‘\(v\)’ at some point during its motion. 

We know that an object has a constant velocity if the net force acting on it is zero. Using this principle on the spherical object we get,

\(
F_g = F_d + F_b\\
\begin{array}{ll}
\mbox{here,} & F_g\mbox{ – is gravitational force acting on the object}\\
& F_d\mbox{ – is drag force acting on the object}\\
& F_b\mbox{ – is the buoyant force on the object by the liquid}\\
\end{array}
\)

\(
mg = 6\pi\eta rv + F_b\\
\begin{array}{lll}
\mbox{here,} & m\mbox{ – is mass of the object}\\
& g\mbox{ – is acceleration due to gravity}\\
& \eta, v \mbox{ and } r\mbox{ have their usual meaning}\\
\end{array}
\)

By isolating ‘\(v\)’ we get,

=> \(\frac{mg – F_b}{6\pi\eta rv} …(1)\)

Mass ‘m’ of the object in terms of its volume and density can be written as,

\(m = \frac{4}{3}\pi r^3 \rho_{s}\); here \(\rho_s\) is density of the spherical object \( …(2)\)

The buoyant force on the object by the liquid is,

\(F_b = \frac{4}{3}\pi r^3 \rho_{l}\); here \(\rho_l\) is density of the liquid \( …(3)\)

Substituting equations (2) and (3) in (1),

\(
=> [\frac{4}{3}\pi r^3\rho_{s}g – \frac{4}{3} \pi r^3 \rho_l]/6\pi \eta r = v\\
=> [\frac{4}{3} \pi r^3(\rho_{s}g – \rho_l)]/6\pi \eta r = v\\
=> v = \frac{4}{3} \pi r^3[(\rho_{s}g – \rho_l)/6\pi \eta r]\\
=> v = [2r^2(\rho_{s}g – \rho_l)/9\eta]\\
\)

Therefore, \(v = \frac{2}{9}[r^2(\rho_{s}g – \rho_l)/9\eta]\) is the terminal velocity equation.

Applications

1. Stokes law is used in Hydrocyclones and Centrifuges.

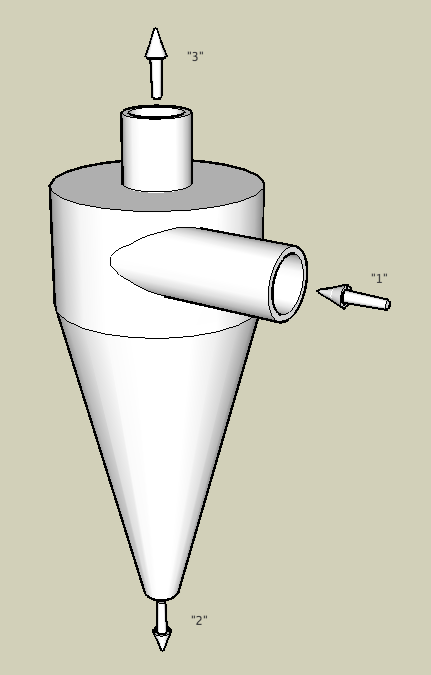
2. Stokes law is also used in settling pits in order to separate drilling mud from the desired drilling material, like limestone.
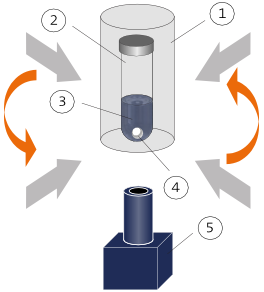
3. A machine called API oil-water separator is used to separate water from oil, in oil refineries and petrochemical plants, etc.
4. The principal used in a Falling-Sphere Viscometer is also stokes law.

5. Water droplets falling in rain also follow stokes law.
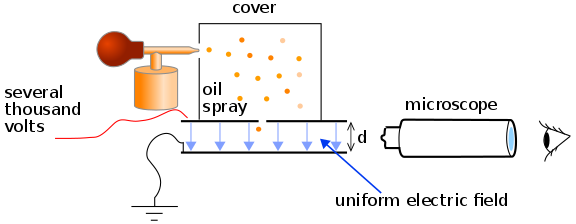
6. Stokes law was used in calculating the charge of an electron in Millikan’s oil drop experiment.

Examples

Question 1. A solid metal ball is falling in a long liquid column and has attained terminal velocity = 2 m/s. Find the viscosity of the liquid if the radius of metal ball is r = 5 cm and its density \(\rho_s\) = 8050 \(kg/m^3\) (density of liquid l = 1000 \(kg/m^3\) and g = 10 \(m/s^2\)). 

Answer. Given, radius of the sphere(\(r\)) = 5 cm = 0.05 m

density of the sphere (\(\rho_s\)) = 8050 \(kg/m^3\)

terminal velocity(\(v\)) = 2 m/s

Let, viscosity of the liquid be ‘\(\eta\)’ 

Using the terminal velocity equation, \(v = \frac{2}{9}[r^2(\rho_{s}g – \rho_l)/9\eta]\)

Substituting the values of the \(\eta, v \mbox{ and } r\) in the equation,

\(
=> 2 = \frac{2}{9}[(10)(0.05)^2(8050 – 1000)/9\eta]\\
=> 9 = [25 * 10^{-3} * 7050]/9\eta\\
=>\eta = (176250 * 10^{-3})/81\\
=> \eta = 2.18 kg/ms
\)

Question 2. A platinum metal ball of radius r = 6 cm and density \(\rho_p\) = 21450 \(kg/m^3\) is released at the top of a long mercury column of density m = 13600 \(kg/m^3\) to fall under gravity. Then find the terminal velocity obtained by this platinum ball (viscosity of the mercury column, = 0.0015 and g =10 \(m/s^2\)).

Answer. We have a platinum ball of, radius(\(r\)) = 6cm = 0.06m

density of the ball (\(\rho_p\)) = 21450 \(kg/m^3\)

The mercury column has, density(\(\rho_m\)) = 13600 \(kg/m^3\)

viscosity(\(\eta\)) = 0.0015 kg/ms

Substituting the given values in the terminal velocity equation,

\(
v = \frac{2}{9}[r^2(\rho_{s}g – \rho_l)/9\eta]\\
=> v = \frac{2}{9}[(10)(0.06)^2(21450 – 13600)/9(0.0015)]\\
=> v = \frac{2}{9}[(36 * 10^{-3} * 7850)/(135 * 10^{-4})]\\
=> v = 4491.85 m/s
\)

FAQs