The Arrhenius Equation is an equation to measure the temperature dependence of the rate of reaction. It has a significant application in determining the rate of a chemical reaction and also plays a major role in calculating the energy of activation.
The Arrhenius equation is actually used to find the rate constant(k) of a reaction at a given temperature. Then we can use the following equation to find the rate of reaction.
rate = \(k * [\mbox{conentration}]^{n}\)
where,
k – rate constant (quantifies the rate and direction of a chemical rea6ction)
n – order of reaction,
From the above equation, we can observe that the rate of the reaction depends directly on the rate constant k, given that the concentration of the reaction and the order of the reaction is constant.
Thus, Arrhenius equation establishes a relation between the temperature of the reaction and the rate of the reaction..
Index
History
Swedish scientist, Svante Arrhenius proposed the Arrhenius equation in 1889. It was based on the work of Dutch chemist Jacobus Henricus van’t Hoff (the van’t Hoff equation) in 1884.

Arrhenius Equation
Now, let us have a look at the Arrhenius Equation and its terms.
\(k = A e^{-\frac{E_{a}}{RT}}\)
where,
k – Rate Constant. It Quantifies the rate and direction of a chemical reaction.
T – Absolute Temperature (Taken in Kelvin)
A – Arrhenius constant / pre-exponential factor / Frequency factor.
It deals with the collisions between molecules and can be thought of as the number of correctly oriented collisions between reactant molecules which can lead to products.
The units of A are identical to those of the rate constant, k, and will vary depending upon the order of the reaction.
For the 1st order reaction, the units are s-1.
For the 2nd order reaction, the units are L mol-1s-1.
Ea – Activation Energy of reaction. It is basically, the minimum energy required for reactants to transform into products.
A – Universal Gas Constant (8.314 J mol-1 K-1 in SI units).
e is the Euler’s number (approximately equal to 2.718).
The exponential part of the equation represents the fraction of collisions that have enough energy to overcome the activation barrier, at temperature, T.
Alternatively, the equation may be expressed as
where Ea is the activation energy for the reaction (in the same units as kBT),
kB is the Boltzmann constant.
From the equation, we can deduce that as temperature(T) increases, the rate constant(k) increases, for a constant Activation Energy.
T ∝ k
Arrhenius Plot
Taking the logarithm of Arrhenius equation, we get,
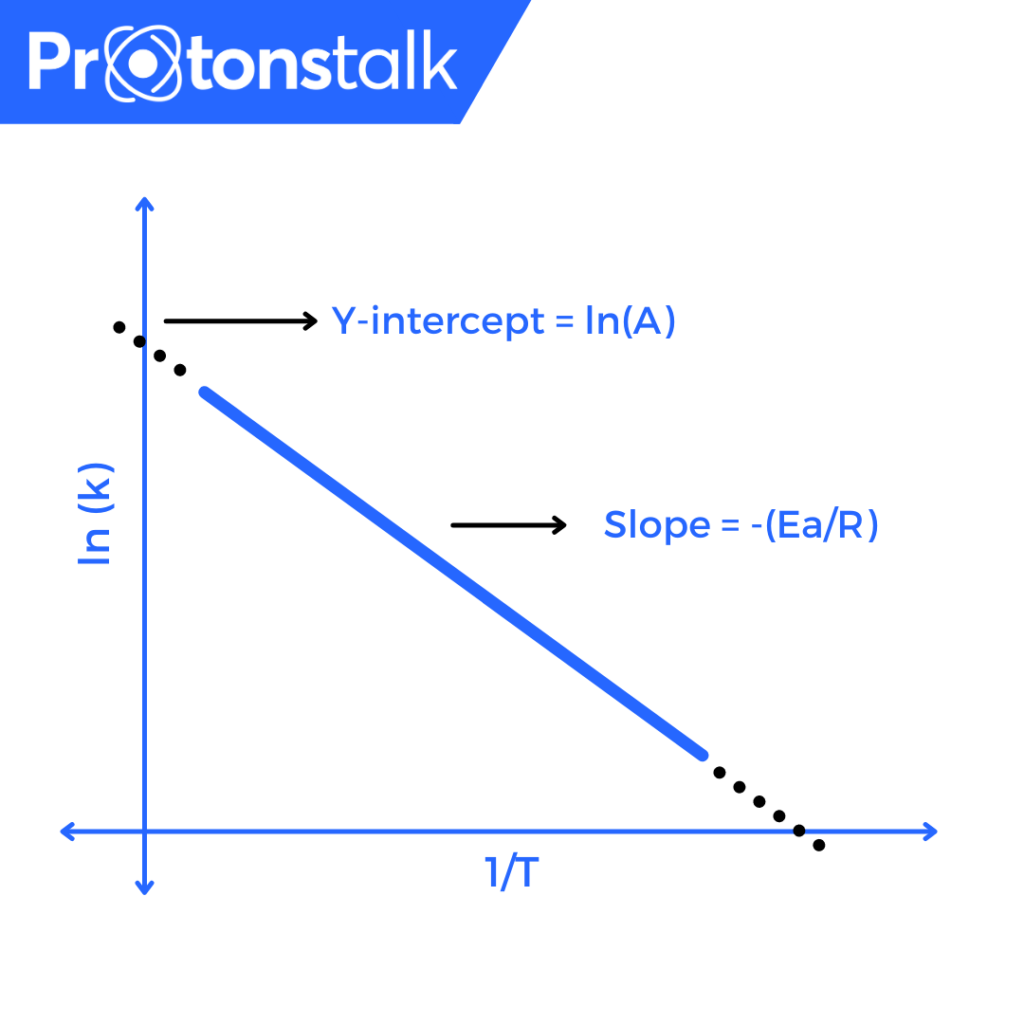
\(\ln(k) = \ln(A) – \frac{E_{a}}{R}(\frac{1}{T})\) (Another Form Of Arrhenius Equation)
Rearranging the terms we get,
\(\ln(k) = -\frac{E_{a}}{R}(\frac{1}{T}) + \ln(A)\)
This has the same form as an equation of the straight line,
\(y = mx + b\)
Hence, a plot of ln(k) versus \(T^{-1}\) gives a straight line, whose slope and intercept could be used to calculate \(E_{a}\) and ln(A).
m = slope = \(E_{a}\) / R
b = Intercept = ln(A)
Arrhenius Equation For Two Reactions
\(\log(k) = \log(A) – \frac{E_{a}}{2.303RT}\)
Suppose, we have two reactions.
\(\ln(k_1) = \ln(A) – \frac{E_{a}}{R}(\frac{1}{T_1})\)
\(\ln(k_2) = \ln(A) – \frac{E_{a}}{R}(\frac{1}{T_2})\)
We could find one of k1, k2, T1, T2, given that we know the values of the other three variables. How? Let us see.
Subtracting the above two equations,
\(\ln(k_1) – \ln(k_2) = \frac{E_{a}}{R}(\frac{1}{T_2} – \frac{1}{T_1})\)
“or” we can write above equation as:
\(\frac{k_1}{k_2} = e^{\frac{E_{a}}{R}(\frac{1}{T_2} – \frac{1}{T_1})}\)
Arrhenius Equation Applications
- Arrhenius Equation can be used to find out the optimum temperature at which maximum product is obtained.
- It is also used to calculate the activation energy based on the rate of the reaction.
Get to know about a similar equation called Eyring Equation
Examples
Question 1. The activation energy of a chemical reaction is 100kJ/mol and its A factor is 10 M-1s-1. Find the rate of constant at a temperature of 300 K.
Solution. Given,
Ea = 100KJ/mol
A = 10 M-1s-1
T = 300 K
As we know,
\(\ln(k) = \ln(A) – \frac{E_{a}}{RT}\)
Substituting the above given values in the eq,
\(\ln(k) = \ln(10) – \frac{100000}{8.314*300}\)
∴ ln(k) = -37.8
∴ k = \(3.834 * 10^{-17}\)
Question 2. Given the following graph of log(k) vs 1/T. If the slope is ‘a’ degrees and the y-intercept is ‘c’ find out \(E_{a}\) and A of the reaction.
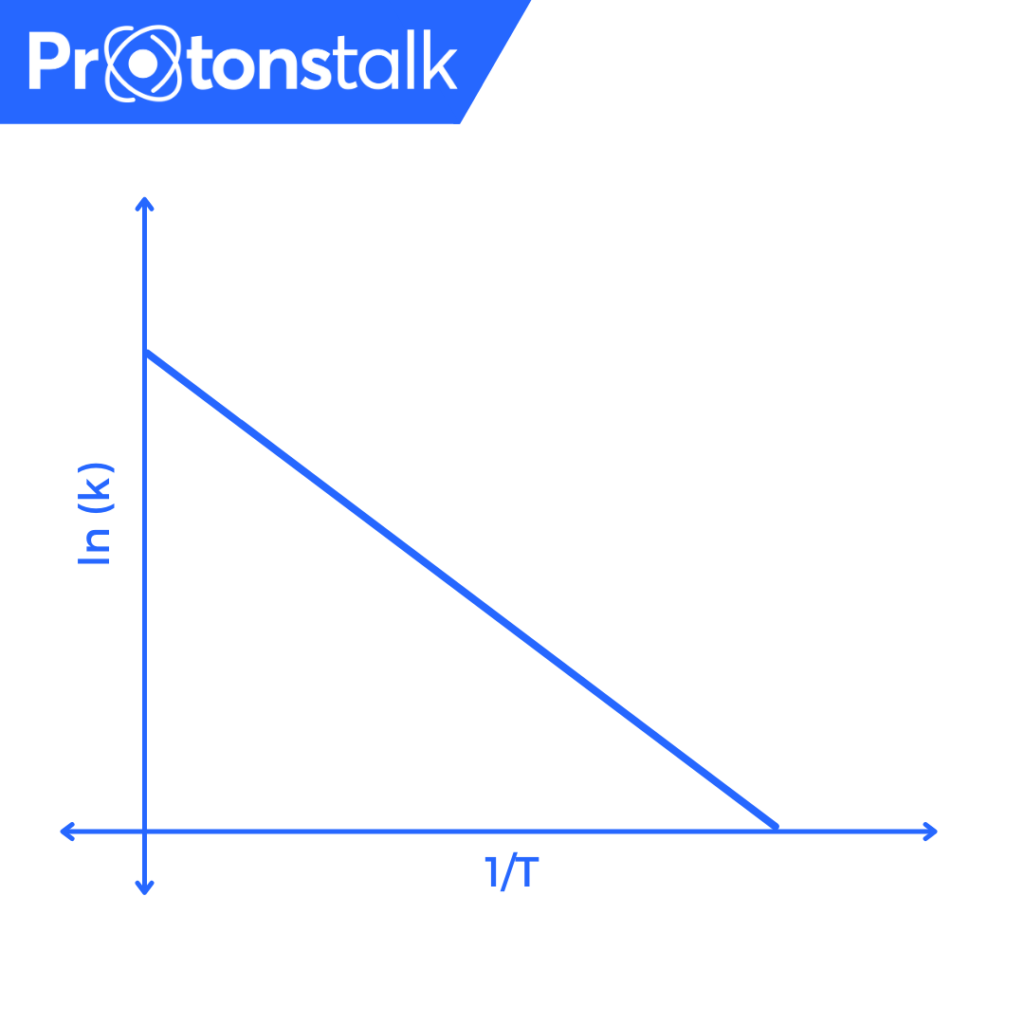
Solution. As we know,
\(\ln(k) = \ln(A) – \frac{E_{a}}{RT}\)
This is of the form,
\(y = mx + c\\
m = \tan(a) = -\frac{E_a}{R}\\
c = \ln(A)\\
∴ E_a = -R\tan(a)\\
∴ A = e^c\\
\)
FAQs
It is the minimum energy required for reactants to transform into products. It is denoted by Ea. The SI units for activation energy are joules (J) and or kilo-joules per mole (kJ/mol) or kilo-calories per mole (kcal/mol).
The symbol ‘A’ is the frequency factor or the Arrhenius factor. It deals with the collisions between molecules and can be thought of as the frequency of correctly oriented collisions between molecules that have sufficient energy to spark a chemical reaction.
The activation energy(Ea) can be calculated from Arrhenius Equation in two ways. It can be determined from the graph of ln(k) vs 1T by calculating the slope of the line. It can also be determined from the equation:
\(E_a = RT(\ln(A) – \ln(k))\)
‘Or’
\(E_a = 2.303RT(\log(A) – \log(K))\)

