Quantum Numbers

We have four quantum numbers in chemistry that are used to describe the state of an electron which includes its distance from the nucleus, the orientation and type of orbital, and its spin. Let us start from the beginning and understand it completely.

Our understanding of atoms, their structure, the electronic configuration has evolved over time. We understood that electrons can’t exist anywhere around the nucleus and there exists a proper electronic configuration that was cited first in Bohr’s atomic model.

Eventually, with the quantum theory and the Schrodinger equation, the concept of electronic configuration also improved. There came four quantum numbers that uniquely differentiate every electron in an atom based on its shell, its subshell, its specific cloud within subshell, and its spin.

So, let us look at these quantum four quantum numbers and how are they connected.

Principal Quantum Number (n)

Denoted by n, Principal Quantum Number describes the principal electron shells or energy levels. It can theoretically have any integral value greater than or equal to 1.

There are only 7 shells that can accommodate all the 118 elements discovered till now. These quantum numbers are represented with uppercase alphabets starting from K, L, M, N, and so on.

So, n = 1 -> K, n = 2 -> L
n = 3 -> M, n = 4 -> N and so on

An electron shell with Principal Quantum Number (n) can accommodate 2n² electrons

The most probable distance of the electron from the nucleus depends on this quantum number, as the number increase, the distance increases.

Coming to energy, you would require more energy to remove an electron from 1st orbit when compared to higher orbits.

As n increases the size of the shell also increases.

Azimuthal Quantum Number (l)

Denoted by l, this quantum number describes a subshell. It is also called as Angular Quantum Number or Orbital Quantum Number. The values of l range from 0 to n-1 and thus depends on its principal shell.

Every value of this quantum number have a lowercase alphabet starting from s, p, d, f and so on.

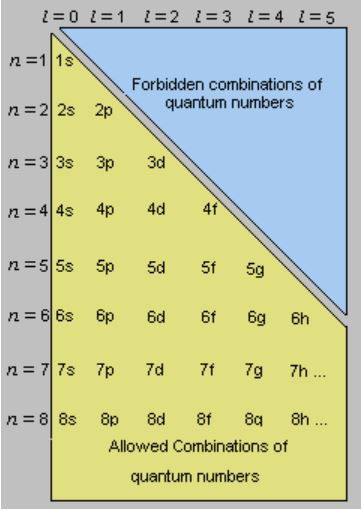
So l = 0 -> s
l = 1 -> p
l=2 -> d
l=3 -> f and so on

There is a restriction on the combinations of principal quantum number and azimuthal quantum number, the image shows the theoretically possible combinations.

A subshell with Azimuthal Quantum Number (l) can accommodate 2(2l+1) electrons.

This quantum number l gives the magnitude of the orbital angular momentum through the relation.

L² = ħ² ℓ (ℓ + 1)

This quantum number also gives us the shape of the orbital as shown in the the table at the end.

Magnetic Quantum Number (m_l)

Denoted by m_l, this quantum number describes the specific orbital in that subshell. The values of this quantum number range from -l to +l, so there are 2l +1 orbitals in a subshell. So, this quantum number depends directly on l and indirectly on n

These orbitals are represented with a specific subscript to the subshell depending on the orientation of the orbital. as given below

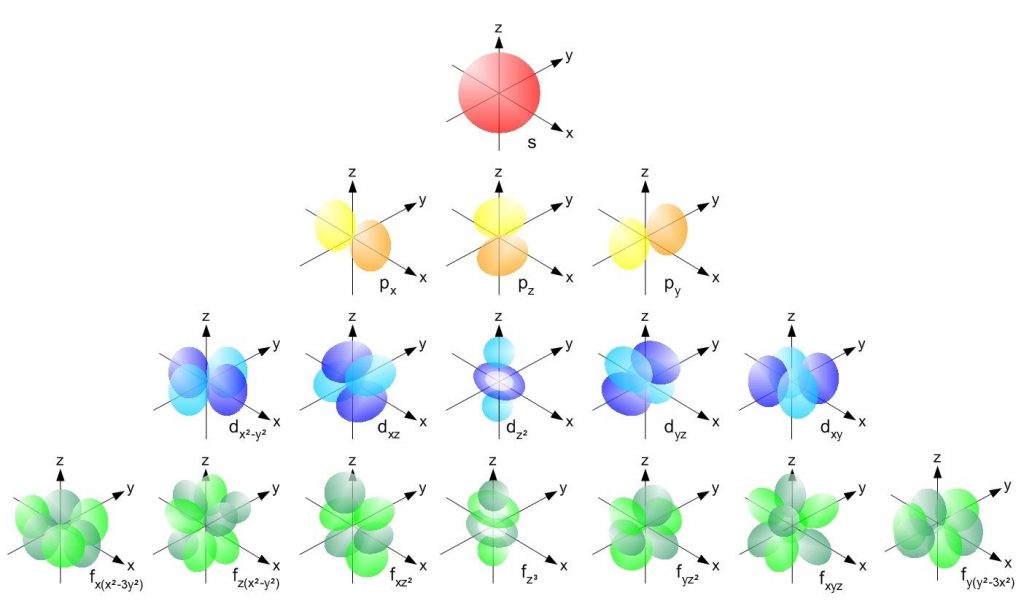
Every orbital here can accommodate 2 electrons.

Spin Quantum Number(m_s)

Denoted by m_s, this quantum number describes the spin of an electron. There are two spin quantum numbers that are +1/2 for upward spin and -1/2 for downward spin. This quantum number is independent of the above three quantum numbers.

As we saw above, there are two electrons in each orbital, the spin quantum number helps to differentiate these two electrons. According to Pauli’s Exclusion Principle, the two electrons in an orbital must have different spin quantum numbers.

The value of the electron spin quantum number determines whether the atom in question has the ability to produce a magnetic field.

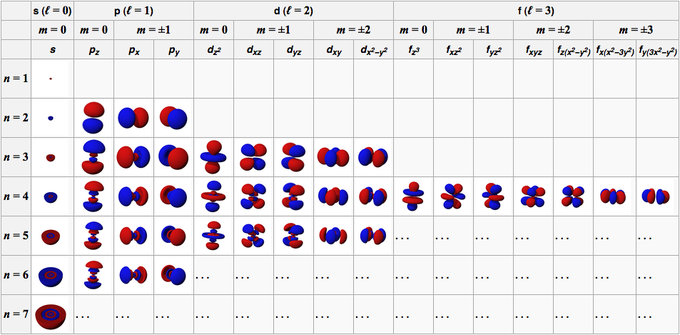
So, those were the four different quantum numbers used to differentiate every electron in an atom. Hope you would have got a good idea regarding them.

FAQs

Related Topics