Mean proportional is another term for geometric mean. Geometric mean is a measure of central tendency, like the arithmetic mean. It is calculated differently, however. It is a common measurement in ratios and proportions.
Index
How to Calculate Mean Proportional
Here, we are going to discuss how the mean proportional is defined, and how to calculate it.
Definition and Formula
For two real, positive numbers \(a\) and \(b\), the geometric mean (also known as mean proportional) is the number \(x\) satisfying:
\(\frac{a}{x} = \frac{x}{b}\)
In other words,
\(x = \sqrt{ab}\)
Note that the term inside the square root must be positive for this formula to work.
Mean Proportional Between Two Numbers
As we have seen above, to calculate the mean proportional between two numbers \(a\) and \(b\) we have to:
- Take the product of the two numbers, \(ab\)
- Take the square root of this product.
This gives us the mean proportional between the two numbers, or the geometric mean.
Applications of Mean Proportional
Geometric Mean Altitude Theorem
In a right angled triangle ABD, if we drop a perpendicular AC onto hypotenuse BD, we have:
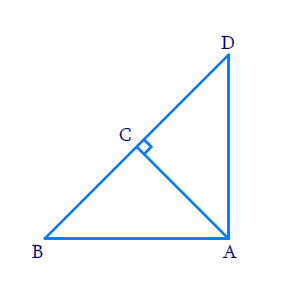
\(\angle ACD = \angle DAB = 90 \circ\)
As well as,
\(\angle ADB = \angle BAC\)
Thus, by AA similarity criterion,
\(\triangle ADB \sim \triangle CDA \sim \triangle CAB\)
This gives us, by definition of similarity,
\(\frac{CD}{AC} = \frac{AC}{CB}\)
In other words, AC is the geometric mean of CD and CB.
\(AC = \sqrt{CD\cdot CB}\)
We can get CD and CB from similar relations:
\(\frac{CD}{DA} = \frac{DA}{DB}\)
Or,
\(CD = \frac{{(DA)}^2}{DB}\)
Similarly,
\(CB = \frac{{(AB)}^2}{DB}\)
Solved Examples
Question 1. Calculate the mean proportional between 234 and 104.
Solution. Here, we can write \(a\) = 234, \(b\) = 104. Then, by definition of geometric mean,
\(x = \sqrt{ab}\)
Substituting \(a\) and \(b\), we have,
\(x = \sqrt{234 \cdot 104}\)
\(x = \sqrt{24336} = 156\)
Thus, the geometric mean of 234 and 104 is 156.
Question 2. Calculate the length of altitude on hypotenuse, for a triangle with sides 3 cm, 4 cm and 5 cm.

Solution. Using above figure again for reference, let AB = 3 cm, AD = 4 cm, DB = 5 cm.
From Geometric Mean Altitude Theorem, we know that the altitude AC is given by,
\(AC = \sqrt{CD \cdot CB}\)
We obtain CD and CB separately as follows:
\(CD = \frac{{(DA)}^2}{DB}\)
\(CD = \frac{16}{5} = 3.2\)
And,
\(CB = \frac{{(AB)}^2}{DB}\)
\(CB = \frac{9}{5} = 1.8\)
So we now have altitude AC as,
\(AC = \sqrt {1.8 \cdot 3.2} = \sqrt{5.76} = 2.4\)
Thus, the length of the altitude is 2.4 cm.
FAQs
The mean proportional x of A and B is defined as (x = \sqrt{A \cdot B}).
The mean proportional or geometric mean \(x\) of 4 and 9 is given by,
\(x = \sqrt{4 \cdot 9} = \sqrt{36}\)
\(x = 6\)
Thus, 6 is the geometric mean of 4 and 9.
The ratios a:b and b:c are in continued proportion if,
\(\frac{a}{b} = \frac{b}{c}\)
Then c is called the third proportion of a and b, while b is the geometric mean of a and c.
Let x be the third proportional of 16 and 32. In other words, 32 is the mean proportional of 16 and x. Then we have,
\(\frac{16}{32} = \frac{32}{x}\)
Or,
\(x = \frac{32^2}{16} = 64\)
Thus, the third proportional of 16 and 32 is 64.
Related Topics:
