Lamis Theorem is used on a body under the influence of 3 forces, or when three forces are acting on a body.
Index
Lamis Theorem Statement
“When three forces acting at a point are in equilibrium, then each force is proportional to the sine of the angle between the other two forces.”
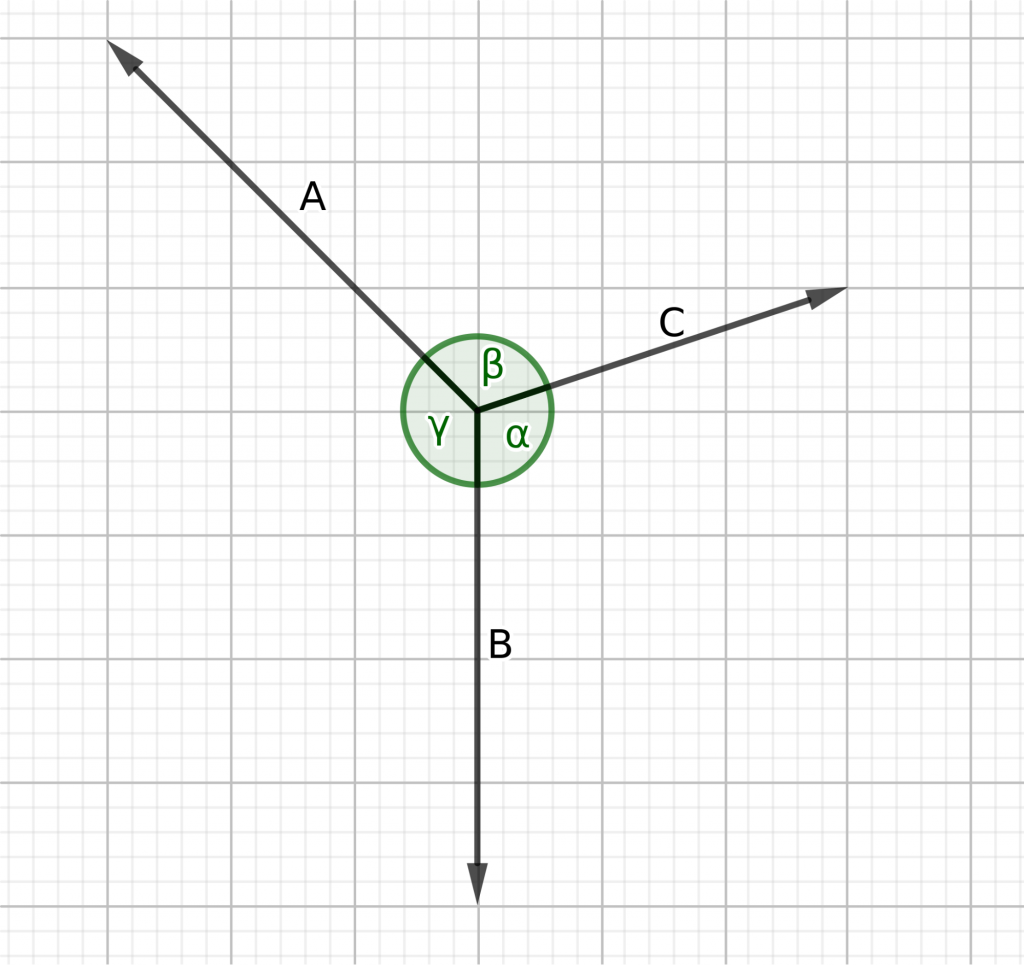
Consider three forces \(A, B \,\&\, C\).
These forces are acting on a particle or a rigid body.
Since these three forces are making three different angles, we name them \(\alpha, \beta \,\&\, \gamma\).
Let’s assume that;
\(\alpha\) be the angle between forces C & B
\(\beta\) be the angle between forces A & C
\(\gamma\) be the angle between forces B & A
In a mathematical equation, it is expressed as;
\(\frac{A}{\sin \alpha} = \frac{B}{\sin \beta} = \frac{C}{\sin \gamma}\)
Derivation
Let the forces acting on the point be \(F_A, F_B \,\&\, F_C\).
As per the statement, we can derive that
\(F_A + F_B + F_C = 0\)
Now, these force vectors can be made into a triangle and drawn as;
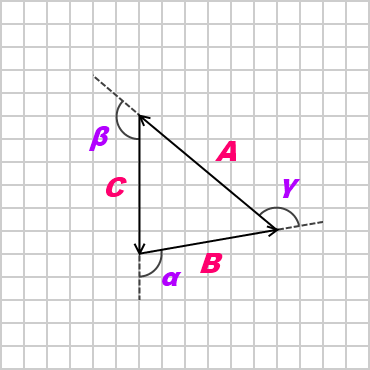
Writing angles in terms of the complementary angle.
Using the law of triangular addition.
Using sine rule we get,
\(\frac{A}{\sin (180 – \alpha)} = \frac{B}{\sin (180 – \beta)} = \frac{C}{\sin (180 – \gamma)}\)
So we get,
\(\frac{A}{\sin \alpha} = \frac{B}{\sin \beta} = \frac{C}{\sin \gamma}\)
Hence, we get the result for Lami’s theorem.
Limitation of Lamis Theorem
There should be three forces acting on an object.
We may not apply Lami’s theorem if there are more or less than three forces.
Lami’s theorem applies to
- Coplanar,
- Concurrent and
- Non-collinear forces.
Application
Lami’s theorem relates the magnitudes of concurrent, coplanar, and non-collinear forces maintaining the static equilibrium of an object. The theorem is extremely useful in analyzing most mechanical and structural systems.
Solved Examples
Question. Consider a cardboard piece hanging with the help of two strings making equal angles with the two nails. Calculate the tension in both strings.
The figure represents the free body diagram. Applying Lami’s theorem we get;
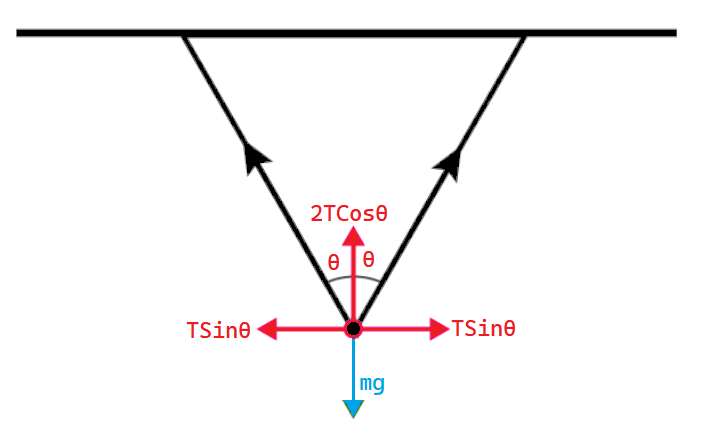
\(\frac{T}{\sin(180 – \theta)} = \frac{T}{\sin(180 – \theta)} = \frac{mg}{\sin 2\theta}\)
Since, \(\sin(180 – \theta) = \sin(\theta) \text{ and } \sin(2\theta) = 2\sin(\theta)\cos(\theta)\)
So we get;
\(\frac{T}{\sin(\theta)} = \frac{mg}{2\sin(\theta)\cos(\theta)}\)
I.e., \(T = \frac{mg}{2 cos(\theta)}\)
FAQs
The lamis theorem states that;
“When three forces acting at a point are in equilibrium, then each force is proportional to the sine of the angle between the other two forces.”
Lami’s theorem is limited to three forces when applied to a body; we cannot apply it if there are more or less forces.
The conditions for applying Lami’s theorem are:
1. There must be exactly three forces must be acting on the body.
2. All the forces acting on the body should be either converging or diverging from the body.
