Bohr Magneton is magnetic dipole moment associated with an atom due to orbital motion and spin of an electron.
The Bohr magneton (symbol \(\mu_B\)) is a physical constant and the natural unit for expressing the magnetic moment of an electron caused by either its orbital or spin angular momentum and is given by:
\(\mu_B = \frac{e\hbar}{2m_e}\)
where,
\(e\) is the elementary charge,
\(\hbar\) is the reduced Planck constant,
\(m_e\) is the electron rest mass,
The value of Bohr magneton in SI units is \(9.27400968(20)×10^{-24}JT^{-1}\)
Index
History
- Walther Ritz (1907) and Pierre Weiss are responsible for the concept of elementary magnets. Several researchers suggested that the magneton should have Planck’s constant h even before the Rutherford model of atomic structure.
- By postulating that the ratio of electron kinetic energy to orbital frequency should be equal to h, Richard Gans computed a value that was twice as large as the Bohr magneton in September 1911.
- In 1911, Romanian physicist Stefan Procopiu discovered the expression for the electron’s magnetic moment. In Romanian scientific literature, the importance is often referred to as the “Bohr–Procopiu magneton.”
- In 1911, the Weiss magneton was discovered to be a unit of magnetic moment equal to 1.531024 joules per tesla, or around 20% of the Bohr magneton.
- As a result of his atom model, the Danish physicist Niels Bohr obtained the values for the natural units of atomic angular momentum and magnetic moment in the summer of 1913.
- Wolfgang Pauli named the it in a 1920 article in which he compared it with the experimentalists’ magneton, which he called the Weiss magneton.
Bohr Magneton Derivation
Consider a magnetic dipole moment as a charge q moving in a circle with radius r with speed v.
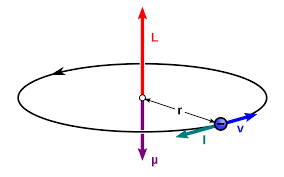
The current is the charge flow per unit time. Since the circumference of the circle is \(2πr\), and the time for one revolution is \(2πr/v\), one has the current as \(I = qv/2πr\).
The magnitude of the dipole moment is
\(|\mu| = I . \mbox{area} \)
\(|\mu| = (qv/2πr)2πr\)
\(|\mu| = qrp/2m\), where p is the linear momentum.
Since the radial vector r is perpendicular to p,
we have \(\mu = (qr × p)/ 2m = qL /2m\),
where L is the angular momentum.
The magnitude of the orbital magnetic momentum of an electron with orbital-angular momentum quantum l is
\(\mu = e\hbar/2m_e [l(l + 1)]1/2 = \mu_B[l(l + 1)]1/2\)
Here, \(\mu_B\) is a constant called Bohr magneton, and is equal to \(\mu_B = e\hbar/2m_e\)
\(\mu_B\) = (1.6 × 10-19C) × (6.626 × 10-34J · s/2π) /2 × 9.11 × 10-31kg
\(\mu_B\) = 9.274 × 10−24J/T
where T is the magnetic field, Tesla.
For the electron, it is the simplest model possible to the smallest possible current to the smallest possible area closed by the current loop.
FAQs
It is a physical constant and the natural unit for describing the magnetic moment of an electron induced by either its orbital or spin angular momentum.
Dimensions of bohr magneton are L2 × electric-current. In SI units, these are the dimensions of the “bohr magneton ” quantity. In electromagnetics, there are other unit systems that can be used to assign various measurements.
It is the magnitude of the magnetic dipole moment of an orbiting electron with an orbital angular momentum of ħ.
