Malus law helps us study of light intensity relation of the polarizer-analyzer. It plays a vital role in understanding the polarization properties of light.
Index
History
The law was named after a french engineer, physicist, and mathematician Etienne-Louis Malus. In the year 1808, he discovered that natural light could be polarized when it was reflected by a glass surface.

Malus Law Explained
Malus law states as following
The intensity of a plane-polarised light that passes through an analyzer varies as the square of the cosine of the angle between the plane of the polarizer and the transmission axes of the analyzer.
Note:
Polarizer: A polarizer is an optical filter that lets light waves of a specific polarization pass through while blocking light waves of other polarizations
Analyzer: An analyzer is a device used to check if the light is plane-polarized or not. It can be considered as a second polarizer.
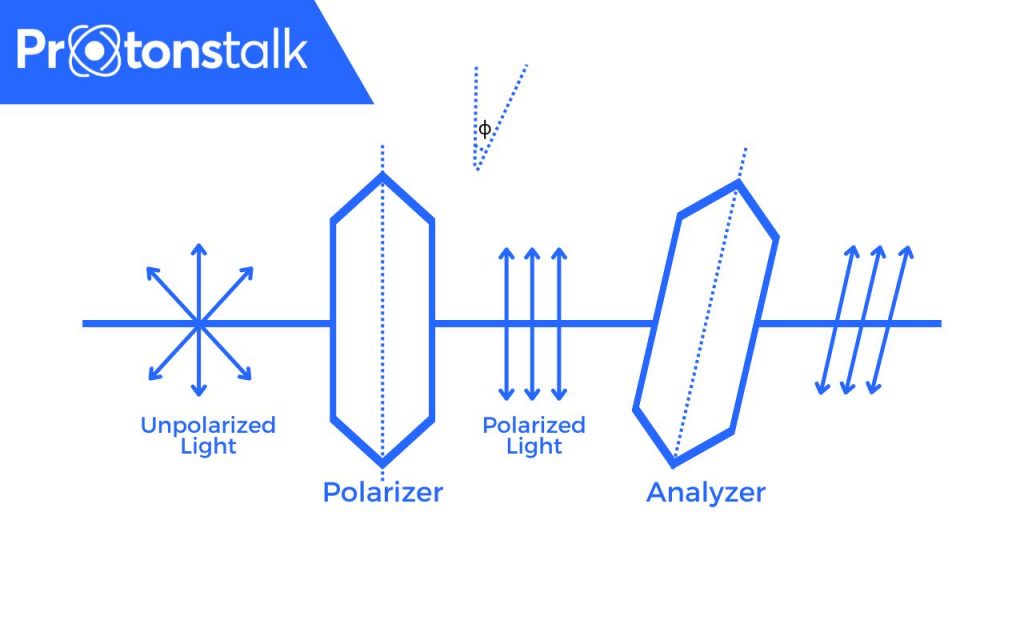
This law is useful in quantitatively verifying the nature of polarised light.
Coming to the expression of Malus law, let us first see two points
- When unpolarized light is incident on an ideal polarizer, the intensity of the transmitted light is exactly half of the intensity of the incident unpolarized light, regardless of how the polarizing axis is oriented.
- An ideal polarizing filter allows 100% of the incident unpolarized light to pass through, which is polarized in the direction of the filter’s polarizing axis.
From the above two points, it can be assumed that,
\(I = I_0 \cos^2 \phi\)Where,
\(I_0\) is the maximum intensity.
I is the
Taking \(I\) to be the average value,
\(<I> = <I_0><\cos^2\phi>\)
⇒ \(\frac{1}{2} = <\cos^2\phi>\)
This satisfies 1st point mentioned above.
For the 2nd point, let us consider \(\phi = 0\)
⇒ \(\cos^2\phi = 1\)
⇒ \(I = I_0\)
As the intensity of an electromagnetic wave is proportional to the square of the amplitude of the wave, the ratio of transmitted amplitude and the incident amplitude is \(\cos^2\phi\).
⇒ \(\cos \phi = \frac{A_{trans}}{A_{max}} = \sqrt{\frac{I}{I_{max}}}\)
= \(\cos^2\phi = \frac{I}{I_{max}}\)
⇒ \(I = I_{max} \cos^2\phi\) (Malus Law Formula)
FAQs
The law of malus states that the intensity of a plane-polarized light that passes through an analyzer varies as the square of the cosine of the angle between the plane of the polarizer and the transmission axes of the analyzer.
Equation:
\(I \propto \cos^2 \phi\)
Unpolarized light has the orientation of the electric field vectors in all possible directions, whereas polarized light has the electric field oriented in a single direction.
