The latus rectum is a special term defined for the conic section. To know what a latus rectum is, it helps to know what conic sections are. Conic sections are two-dimensional curves formed by the intersection of a cone with a plane. They include parabolas, hyperbolas, and ellipses. Circles are a special case of ellipse.
Index
Terminology in Conic Section
Here we discuss some important terminology for conic sections so that we can understand the main concept better.
Focus
The focus ‘or’ foci are fixed points from which the conic sections are constructed. Ellipses and hyperbolas have two foci, while circles and parabolas have one focus each.
Directrix
The directrix is a fixed line that is used to construct a conic section. Every point on the conic is at a certain distance \(PF\) from the focus and \(PM\) from the directrix. The ratio of these distances, \(\frac{PF}{PM}\) is called the eccentricity of the conic and determines its type.
Transverse Axis
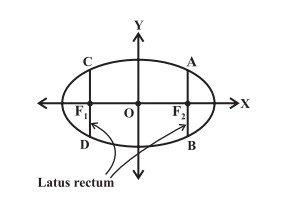
The axis passing through the foci and connecting the vertices of a conic section is said to be the major axis. In the case of the ellipse, this is also called the major axis.
Conjugate Axis
The axis passing through the centre and perpendicular to the transverse axis is said to be the conjugate axis. In the case of an ellipse, this axis is called the minor axis.
Latus Rectum
The latus rectum is the chord that passes through the focus of a conic section, and is parallel to the directrix. For each conic section, the latus rectum has a definite length that can be written in terms of axis lengths as given below
- In case of a circle, the length of latus rectum is equal to the diameter of circle.
- For an ellipse, the length is equal to twice the square of the length of conjugate axis, divided by the length of transverse axis.
- In a parabola, the length is simply four times its focal length.
- In a hyperbola, the length is equal to twice the square of the length of transverse axis divided by the length of conjugate axis.
Formulae
The formulae for each of the cases can be seen as follows.
Ellipse
Let us consider a standard ellipse, centred on the origin, and major axis along the x-axis. Its equation is given by
\(\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\)
Then we have,
- Length of major axis = \(2a\)
- Length of minor axis = \(2b\)
- Separation of foci = \(2c\)
Clearly, the foci are located at \((\pm c, 0)\). Then, we have to find where the ellipse is cut by a chord parallel to the y-axis. Let \(y_0\) be the y-coordinate. We have,
\begin{align}
\frac {c^2}{a^2} + \frac{{y_0}^2}{b^2} & = 1 \\
\Rightarrow \frac{{y_0}^2}{b^2} & = 1 – \frac {c^2}{a^2} \\
\Rightarrow \frac{{y_0}^2}{b^2} & = \frac {a^2 -c^2}{a^2} \\
\Rightarrow \frac{{y_0}^2}{b^2} & = \frac {b^2}{a^2} \\
\Rightarrow {y_0}^2 & = \frac {b^4}{a^2}\\
\Rightarrow y_0 & = \frac {b^2}{a}
\end{align}
\)
Where we have used the relation \(c = \sqrt{a^2-b^2}\).
As the latus rectum is simply equal to twice of this y-value, we have,
\(\text{Length of latus rectum of ellipse} = 2y_0 = \frac {2b^2}{a}\)
Thus, the length of it for an ellipse is simply twice the square of the length of the conjugate axis, divided by the length of the transverse axis.
Circle
As the circle is a special case of the ellipse, with major and minor axis equal in length of the radius \(r\), we have,
\(\text{Length of latus rectum} = \frac {2b^2}{a} = \frac {2r^2}{r} = 2r\)
But as \(2r = d\), the diameter of the circle, we have,
\(\text{Length of latus rectum of circle} = d\)
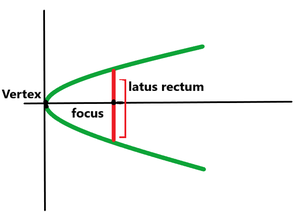
Parabola
Let us consider a standard parabola, with a major axis along the x-axis. Its equation is \(y^2 = 4ax\). The focus is at \((a,0)\). So we draw a line through it, parallel to the y-axis. Let it cut the parabola at \((a,y_0)\).
We have,
\(\begin{align}
{y_0}^2 & = 4a \times a \\
& = 4a^2 \\
\Rightarrow y_0 &= 2a
\end{align}
\)
So the length of the latus rectum must be twice this value, which means,
\(\text{Length of latus rectum of parabola} = 4a\)
Hyperbola
The situation here is very similar to the ellipse. The only difference is that the hyperbola’s equation is either \(\frac{x^2}{a^2} – \frac{y^2}{b^2} = 1\) or \(\frac{y^2}{a^2} – \frac{x^2}{b^2} = 1\). The signs depend on which axis is the transverse axis.
Further, \(c^2 = a^2 + b^2\).
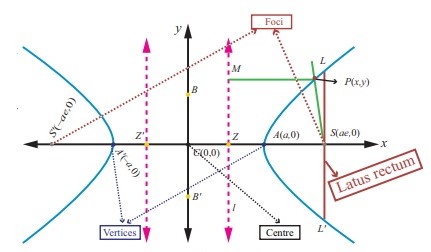
Proceeding with a similar derivation as before, we have the result,
\(\text{Length of latus rectum of hyperbola} = \frac {2b^2}{a}\)
Also Read: Hyperbola vs Parabola
Examples
Question 1. Find the length of latus rectum of a parabola, with focus at (0,2) and directrix as \(y = -2\).
Solution. This parabola has major axis along y-axis. This means that the focus is at \((0,a)\).
Comparing with given focus, we get, \(a = 2\).
As length of latus rectum is \(4a\), the length in this case is \(4 \times 2 = 8\) units.
Question 2. Find the equation of the ellipse with length of latus rectum as 2 units, and focii at \((\pm 2\sqrt{3} , 0)\).
Solution. This ellipse has major axis along x-axis.
We know, in such a case,
Length of latus rectum of ellipse = \(\frac {2b^2}{a}\)
Thus, \(\frac {2b^2}{a} = 2\) Or, \(b^2 = a\)
Further, the foci are located at \((\pm c, 0)\). Equating to given values, we have, \(c = 2\sqrt{3}\)
But, we know that \(c^2 = a^2 – b^2\), so,
\({2\sqrt{3}}^2 = a^2 – b^2\)
Using \(b^2 = a\) from above, we have, \(a^2 – a = 12\)
Solving for a, and taking only positive value, we have, \(a = 4\)
Further, \(b = 2\)
Thus the equation of the ellipse must be,
\(\frac{x^2}{16}+\frac{y^2}{4} = 1\)
FAQs
The formula of latus rectum depends on which conic we are talking about. Using all standard equations, the length of latus rectum:
1. For ellipse = \(2 \frac{b^2}{a}\)
2. For circle = \(2r\)
3. For parabola = \(4a\)
4. For hyperbola = \(2 \frac{b^2}{a}\)
Yes, all conic sections have latus rectum. It is the chord that passes through the focus, and is parallel to the directrix.
In standard form, with the major or transverse axis being x-axis, the endpoints share the same x-coordinate as the focus. The y-coordinates are found by substituting the x-value in the equation of conic section.
If the y-axis is the major axis, the case is reversed. The y-coordinate of the endpoints and the focus are the same. The x-coordinate can be found as above.
In standard form, the length of latus rectum is \(4a\), for all parabolas. Now we need to know two things:
1. What is the axis of the parabola?
2. What direction does it open in?
Based on that, we have four possible equations:
If x-axis is the major axis, and it opens along +x, the equation is \(y^2 = 4ax\).
And if x-axis is the major axis and it opens along -x, the equation is \(y^2 = -4ax\).
If y-axis is the major axis and it opens along +y, the equation is \(x^2 = 4ay\).
And if y-axis is the major axis and it opens along -y, the equation is \(x^2 = -4ay\).
