Apollonius Theorem is an important theorem in Geometry. It connects the lengths of the sides of a triangle, to the lengths of the medians.
Index
What is Apollonius Theorem?
The median of a triangle is the line segment connecting a vertex of a triangle to the midpoint of the opposite side. Apollonius Theorem connects the length of the median to the lengths of the bisected side and the other two sides.
It is equivalent to the Parallelogram Law of Elementary Geometry.
Apollonius Theorem Formula
Let \(a\), \(b\) and \(c\) be the lengths of three sides of the triangle and \(d\) be the length of a median that bisects side \(a\). Let \(m = \frac{a}{2}\), be the length of the bisected half.
Then, Apollonius Theorem states that:
\(c^2 + b^2 = 2(m^2 + d^2)\)
This is called the Apollonius’ Theorem Formula.
In other words, the sum of squares of two sides is equal to twice the sum of squares of the median between them and half of the third side.
Derivation of Apollonius Theorem
We can derive and give Apollonius Theorem proof using the Law of Cosines. Consider the figure below, using the same notation as previously.
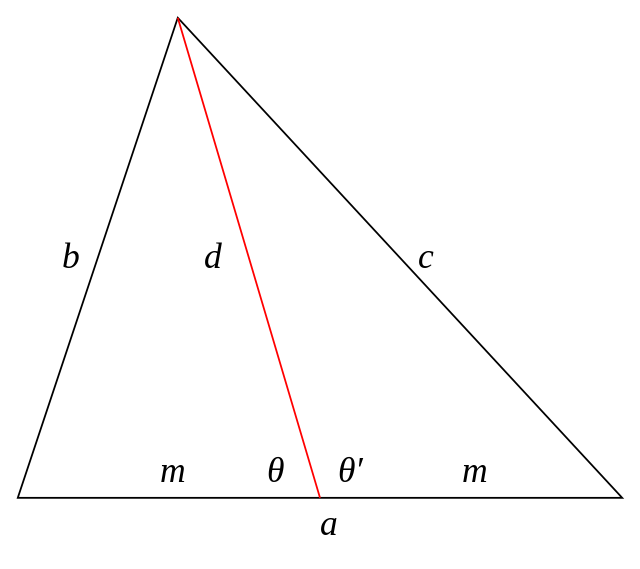
Let median $d$ make angle \(\theta\) on the side facing \(b\) and angle \(\theta ’\) on the side facing \(c\).
Then, for the triangle with sides \(b\), \(d\) and \(m\), we have by Law of Cosines,
\(b^2 = d^2 + m^2 – 2md \cos{\theta}\)
Now, for the triangle with sides \(c\), \(d\) and \(m\), we similarly get,
\(c^2 = d^2 + m^2 – 2md \cos{\theta^\prime}\)
But now, \(\theta + \theta^\prime = \pi = 180^\circ\)
So, \(\cos{\theta^\prime} = -\cos{\theta}\), which we use in the equation connecting \(c\), \(d\) and \(m\).
Thus we get,
\(c^2 = d^2 + m^2 + 2md \cos{\theta}\)
Now, we add this to the first equation, with \(b\), \(d\) and \(m\), so the \(\cos\) terms cancel, giving,
\(c^2 + b^2 = 2(m^2 + d^2)\)
Which proves Apollonius Theorem Formula.
Applications
Apollonius’ Theorem is a theorem in elementary geometry, similar to Pythagoras Theorem. It is useful to calculate the lengths of a median of a triangle.
It is equivalent to the Parallelogram Law, as stated before. This means that it can be used to find the lengths of one diagonal of a parallelogram if the other diagonal and two sides are given.
It is also a special case of Stewart’s Theorem, which deals with the more general situation of a cevian. A cevian, like a median, is a line segment that connects one vertice and the opposite side of a triangle. Unlike a median, however, it need not bisect the other side.
Solved Examples
Question 1. A triangle has sides 7, 6 and 10 cm. Find the length of the median to the side of length 10 cm.
Solution. From the terminology given above, \(a = 10 \text{ cm}, b = 7 \text{ cm}, c = 6 \text{ cm}\).
As the 10 cm side is bisected, we have, \(m= \frac{a}{2} = 5 \text{ cm}\). Let the length of the median be \(d\).
Apollonius Theorem Formula states that,
\(c^2 + b^2 = 2(m^2 + d^2)\)
Substituting required values, we have,
\(6^2 + 7^2 = 2(5^2 + d^2)\)
Which gives,
\(36+49 = 2(25+d^2) \\
85 – 50 = 2d^2 \\
2d^2 = 35 \\
d = \sqrt{\frac{35}{2}} \\
d = 4.183 \text{ cm} \\
\)
Thus, the length of the median is \(d = 4.183 \text{ cm}\).
Question 2. A parallelogram has sides 6 cm and 4 cm. If one diagonal is 8 cm long, find the length of the other diagonal.
Solution. This situation is very similar to the case of a triangle. The two sides and one diagonal form three sides of a triangle. The other diagonal is a median which bisects the first diagonal. The second diagonal is also bisected by the first.
So we have to find length of median and multiply by 2 it to get length of second diagonal.
Using same notation as usual, we have,
\(a = 8 \text{ cm}, b = 6 \text{ cm}, c = 4 \text{ cm}, m= \frac{a}{2} = 4 \text{ cm}\).
Using the formula for Apollonius Theorem, we have,
\(c^2 + b^2 = 2(m^2 + d^2) \\
16+36 = 2(16+d^2) \\
52 – 32 = 2d^2 \\
2d^2 = 20 \\
d = \sqrt{10} \\
d = 3.16 \text{ cm} \\
\)
But the diagonal in parallelogram is twice the length of median of triangle.
Thus, length of other diagonal \(d^\prime = 2d = 6.32 \text{ cm}\).
FAQs
Apollonius Theorem connects the lengths of sides of triangle, with lengths of median.
In words, it states that the sum of squares of two sides is equal to twice the sum of squares of the median between them and half of the third side.
Mathematically, let \(AB, AC\) be side lengths, and \(AD\) be the median to side \(BC\). We can write,
\(AB^2 + AC^2 = 2(AD^2 + BD^2)\)
This is the Apollonius Theorem.
Apollonius Theorem provides us a way of calculating median lengths in triangles, if we know their sides. This helps us solve the triangle.
Pythagoras’ Theorem can be seen as a special case of Apollonius’ Theorem, when we have an isosceles triangle.
Let \(AB, AC\) be equal sides of the isosceles triangle.
The median \(AD\) to the other side \(BC\) is also perpendicular to it, so \(\triangle ADB\) is a right triangle.
By Apollonius’ Theorem,
\(AB^2 + AC^2 = 2(AD^2 + BD^2)\)
But \(AB=AC\) so,
\(2AB^2 = 2(AD^2 + BD^2)\)
Dividing throughout by 2, we have,
\(AB^2 = AD^2 + BD^2\)
This is simply Pythagoras’ Theorem in the right triangle \(ADB\).
The median is the line segment from one vertex to opposite side, that bisects the opposite side.
The angle bisector is the line segment from one vertex to the opposite side, that bisects the angle at vertex.
In general, they are not the same, unless the vertex is between equal sides, i.e. in an isosceles triangle.
