An electric current is the rate of flow of charged particles, such as electrons or ions, through an electrical conductor or space. It is measured in Coulombs/second which is named Amperes. In this article, we will see some important current electricity formulas which will also help you in preparation for competitive exams like JEE and NEET.
Index
ELECTRIC CURRENT
\(I_{av}=\frac{\Delta q}{\Delta t}\) and instantaneous current
\(i=\underset{\Delta t \rightarrow 0}{Lim}\frac{\Delta q}{\Delta t}=\frac{dq}{dt}\)ELECTRIC CURRENT IN A CONDUCTOR
\(I=nAeV\)
\(V_{d}=\frac{\lambda}{\tau },\)
\(V_{d}=\frac{\frac{1}{2}(\frac{eE}{m})\tau ^{2}}{\tau }=\frac{1}{2}\frac{eE}{m}\tau,\)
\(I=neAV_{d}\)
CURRENT DENSITY
\(\overrightarrow{J}=\frac{dl}{ds}\overrightarrow{n}\)ELECTRICAL RESISTANCE
\(I=neAV_{d}=neA(\frac{eE}{2m})\tau =(\frac{ne^{2}\tau }{2m})AE\)
\(E=\frac{V}{l}\) so,
\(I=(\frac{ne^{2}\tau }{2m})(\frac{A}{l})V=(\frac{A}{\rho l})V=\frac{V}{R}\Rightarrow V=IR\)
\(\rho\) is called resistivity (it is also called specific resistance) and
\(\rho =\frac{2m}{ne^{2}\tau }=\frac{1}{\sigma },\sigma\) is called conductivity. Therefore current in conductors
is proportional to potential difference applied across its ends. This is Ohm’s Law.
Units
\(R\rightarrow ohm(\Omega),\rho \rightarrow ohm-meter(\Omega -m)\) also called siemens, \(\sigma \rightarrow \Omega ^{-1}m^{-1}\)
Dependence of Resistance on Temperature
\(R=R_{o}(1+\alpha \Theta )\)Electric current in resistance
\(I=\frac{V_{2}-V_{1}}{R}\)ELECTRICAL POWER
\(P=VI\)
\(Energy=\int pdt\)
\(P=I^{2}R=VI=\frac{V^2}{R}\)
\(H=VIt=I^{2}Rt=\frac{V^2}{R}t\)
\(H=I^{2}Rt Joule=\frac{I^2RT}{4.2}Calorie\)
KIRCHHOFF’S LAWS
Kirchhoff’s Current Law (Junction law)
\(\Sigma I_{in}=\Sigma I_{out}\)
Kirchhoff’s Voltage Law (Loop law)
\(\Sigma IR+\Sigma EMF=0\)
COMBINATION OF RESISTANCES
Resistances in Series
\(R=R_{1}+R_{2}+R_{3}+….+R_{n}\) (this means \(R_{eq}\) is greater then anyresistor) ) and
\(V=V_{1}+V_{2}+V_{3}+….+V_{n}\) \(V_{1}=\frac{R_{1}}{R_{1}+R_{2}+….R_{n}}V;V_{2}=\frac{R_{2}}{R_{1}+R_{2}+….R_{n}}V\)Resistances in Parallel
\(\frac{1}{R_{eq}}=\frac{1}{R_{1}}+\frac{1}{R_{2}}+\frac{1}{R_{3}}\)WHEATSTONE NETWORK : (4 TERMINAL NETWORK)
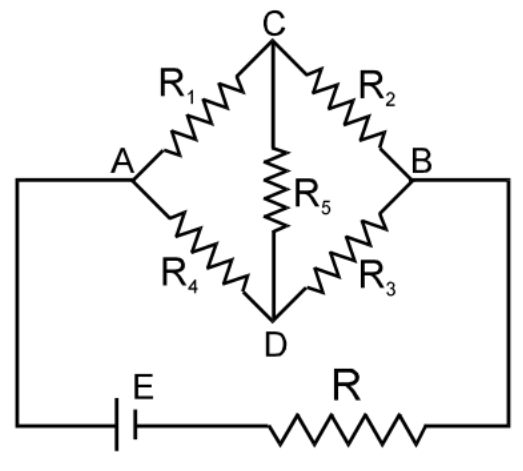
When current through the galvanometer is zero (null point or balance point) \(\frac{P}{Q}=\frac{R}{S}\),then PS = QR.
GROUPING OF CELLS
Cells in Series

Equivalent \(EMFE_{eq}=E_{1}+E_{2}+….+E_{n}\) [write EMF’s with polarity]
Equivalent internal resistance \(r_{eq}=r_{1}+r_{2}+r_{3}+r_{4}….+r_{n}\)
Cells in Parallel

\(\frac{1}{r_{eq}}=\frac{1}{r_{1}}+\frac{1}{r_{2}}+\frac{1}{r_{3}}+….+\frac{1}{r_{n}}\)
AMMETER
A shunt (small resistance) is connected in parallel with a galvanometer to convert it into ammeter. An ideal ammeter has zero resistance.
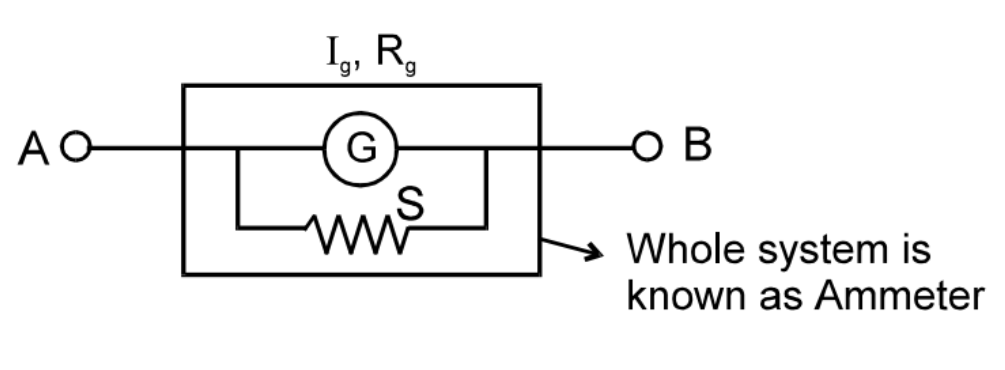
Ammeter is represented as follows –
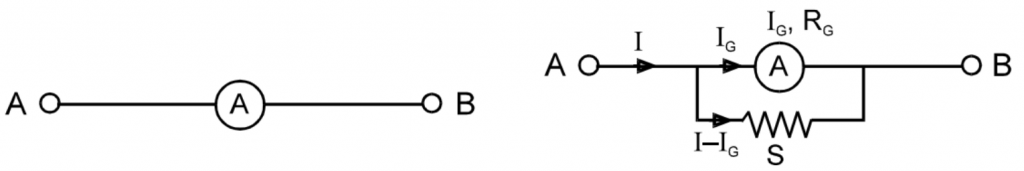
If maximum value of current to be measured by ammeter is I then \(I_{g}.R_{g}=(I-I_{g})S\)
\(S=\frac{I_{g}.R_{g}}{I-I_{g}}\) ; \(S=\frac{I_{g}\times R_{g}}{I}\) when \(I>>I_{g}\)
where I = Maximum current that can be measured using the given ammeter.
VOLTMETER
High resistance is put in series with a galvanometer. It is used to measure the potential difference across a resistor in a circuit.
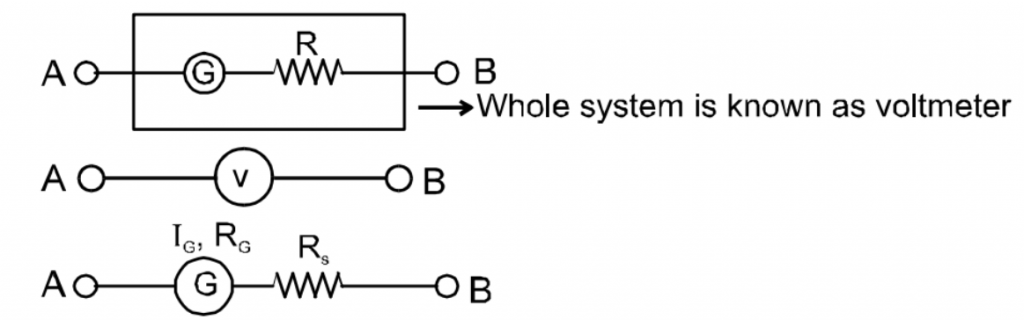
For maximum potential difference \(V=I_{g}.R_{s}+I_{g}R_{g}\)
\(R_{s}=\frac{V}{I_{G}}-R_{G}\) If \(R_{G}<<R_{S}\Rightarrow R_{S}\approx \frac{V}{I_{G}}\)
POTENTIOMETER
\(I=\frac{\varepsilon }{r+R}\)
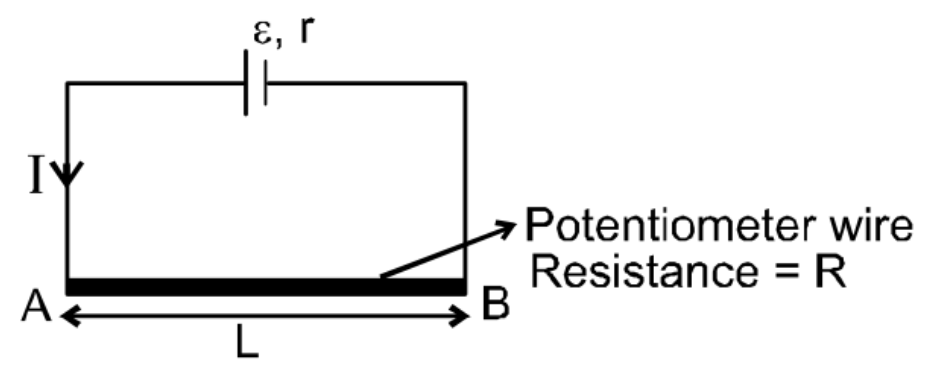
\(V_{A}-V_{B}=\frac{\varepsilon }{R+r}.R\)
Potential gradient \((x)\rightarrow\) Potential difference per unit length of wire
\(x=\frac{V_{A}-V_{B}}{L} =\frac{\varepsilon }{R+r}.\frac{R}{L}\)
Application of potentiometer
(a) To find emf of unknown cell and compare emf of two cells.
In case I, In figure (1) is joint to (2) then balance length =\(l_{1}\)
\(\varepsilon_{1}=xl_{1}\) ……………….(1)
In case II, In figure (3) is joint to (2) then balance length = \(l_{2}\)
\(\varepsilon_{2}=xl_{2}\) ……………….(2)
\(\frac{\varepsilon {1}}{\varepsilon {2}}=\frac{l_{1}}{l_{2}}\)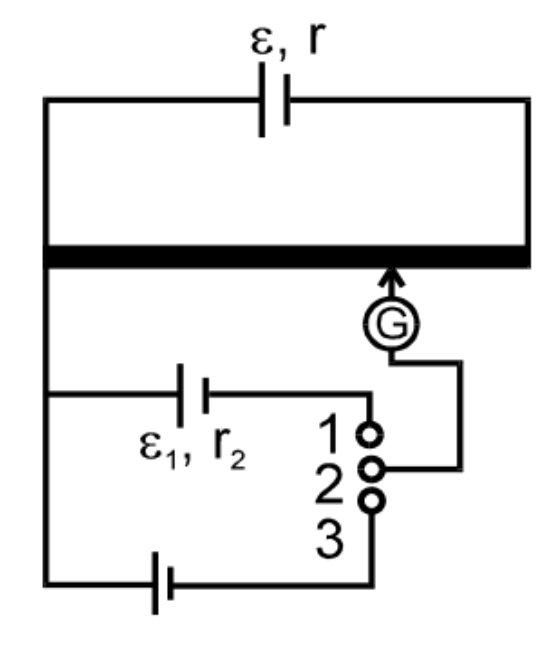
If any one of \(\varepsilon {1}or\varepsilon {2}\) is known the other can be found. If x is known then both \(\varepsilon {1}and\varepsilon {2}\) can be found.
(b) To find current if resistance is known
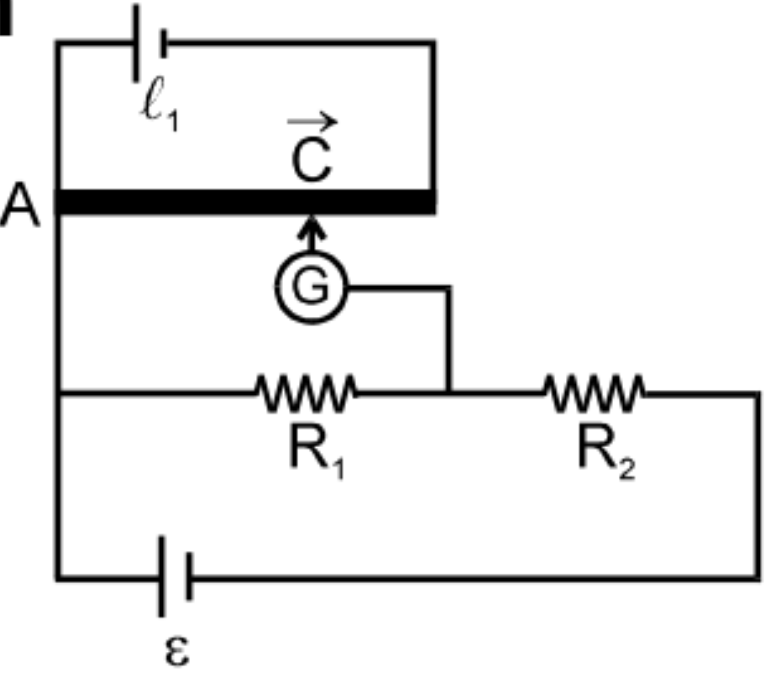
\(V_{A}-V_{C}=xl_{1}\)
\(IR_{1}=xl_{1}\)
\(I=\frac{xl_{1}}{R_{1}}\)
Similarly, we can find the value of \({R_{2}}\) also. Potentiometer is ideal voltmeter because it does not draw any current from circuit, at the balance point.
(c) To find the internal resistance of cell.
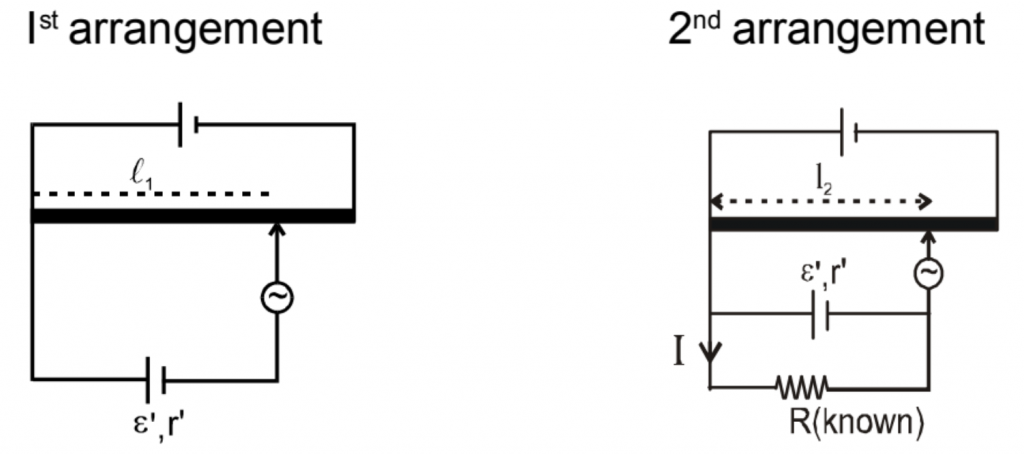
by first arrangement \(\varepsilon ‘=xl_{1}\)……….(1)
by second arrangement \(IR=xl_{2}\)
\(I=\frac{xl_{2}}{R}\), also \(I=\frac{\varepsilon ‘}{r’+R}\)
\(\frac{\varepsilon ‘}{r’+R}=\frac{xl_{2}}{R}\Rightarrow \frac{xl_{1}}{r’+R}=\frac{xl_{2}}{R}\)
\(r’=\left [ \frac{l_{1}-l_{2}}{l_{2}} \right ]R\)
(d) Ammeter and voltmeter can be graduated by potentiometer.
(e) Ammeter and voltmeter can be calibrated by potentiometer.
METER BRIDGE
A Meter bridge is used to measure unknown resistance
If \(AB=lcm,then\) \(BC=(100-l)cm.\)
Resistance of the wire between A and B , \(R\propto l\)
Because,specific resistance \(\rho\) and cross-sectional area A are same for whole of the wire
Or \(R=\sigma l\)……….(1)
where \(\sigma\) is resistance per cm of wire.
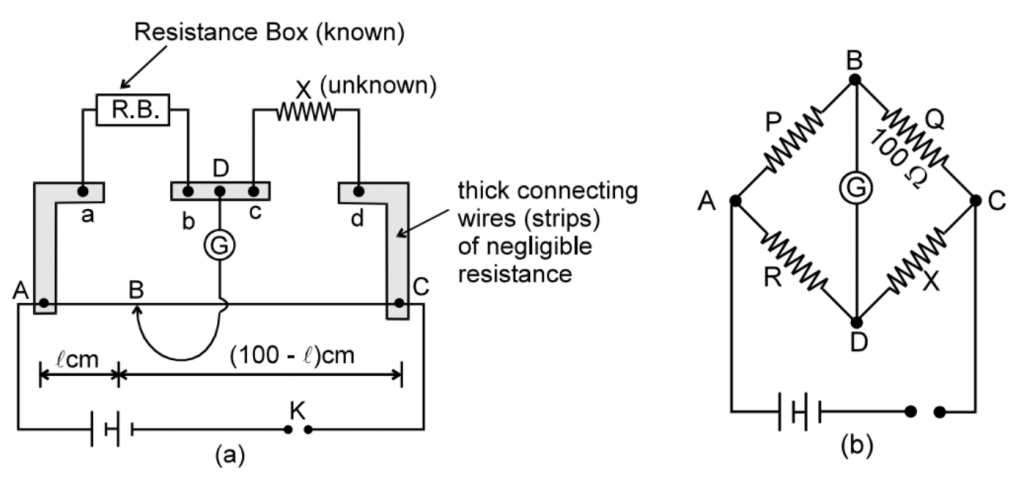
If P is the resistance of wire between A and B then
\(p\propto l\)=\(p=\sigma (l)\)
Similarly, if Q is resistance of the wire between B and C, then
\(Q\propto (100-l)\)
\(Q=\sigma (100-l)\)……..(2)
Dividing (1) by (2), \(\frac{P}{Q}=\frac{l}{100-l}\)
Applying the condition for balanced Wheatstone bridge, we get R Q = P X
Therefore, \( x=R\frac{Q}{P}\) Or \(X=\frac{(100-l)}{l}R\)
Since R and \(l\) are known, therefore, the value of X can be calculated.
