Circular motion is the motion of an object along a circular path. It can be uniform, with a constant angular rate of rotation, or non-uniform with a changing rate of rotation. In this article, we will see some important circular motion formulas which will also help you in preparation for competitive exams like JEE and NEET.
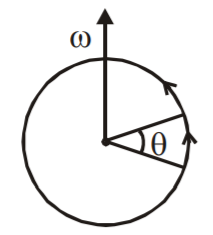
1. Average angular velocity \( \Rightarrow \) \( \omega_{av}=\frac{\Theta_{2}-\Theta_{1}}{t_{2}-t_{1}}=\frac{\Delta \Theta }{\Delta t} \)
2. Instantaneous angular velocity \( \Rightarrow \) \( \omega =\frac{d\Theta }{dt} \)
3. Average angular acceleration \( \Rightarrow \) \( \alpha_{av}=\frac{\omega_{2}-\omega_{1}}{t_{2}-t_{1}}=\frac{\Delta \omega }{\Delta t} \)
4. Instantaneous angular acceleration \( \Rightarrow \) \( \alpha=\frac{d\omega }{dt}=\omega \frac{d\omega }{d\Theta } \)
5. Relation between speed and angular velocity \( \Rightarrow \) \( v=r\omega \) and \( \overrightarrow{v}=\overrightarrow{\omega }\times \overrightarrow{r} \)
6. Tangential acceleration (rate of change of speed)
\( \Rightarrow \) \( a_{t} = \frac{dv}{dt} = r\frac{d\omega }{dt} = \omega \frac{dr}{dt} \)
7. Radial or normal or centripetal acceleration \( \Rightarrow \) \( a_{r}=\frac{v^{2}}{r}=\omega ^{2}r \)
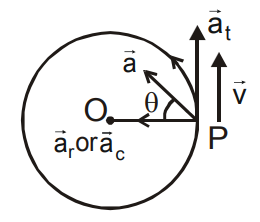
8. Total acceleration
\( \Rightarrow \) \( \overrightarrow{a}=\overrightarrow{a}{t}+\overrightarrow{a}{r} \) \( \Rightarrow \) \( a=\left ( a_{t}^{2}+a_{r}^{2} \right )^{\frac{1}{2}} \)
Where \( \overrightarrow{a}_{t}=\overrightarrow{\alpha}\times \overrightarrow{r} \) and \( \overrightarrow{a}_{r}=\overrightarrow{\omega }\times \overrightarrow{v} \)
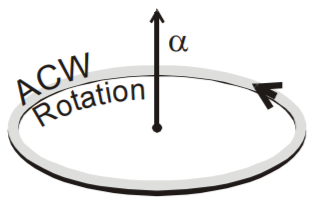
9. Angular acceleration
\( \Rightarrow \) \( \overrightarrow{\alpha }=\frac{d\overrightarrow{\omega }}{dt} \) (Non-uniform circular motion)
10. Radius of curvature R \( =\frac{v^{2}}{a_{\perp }}=\frac{mv^{2}}{F_{\perp }} \) \( \Rightarrow \)
If y is a function of x. i.e. \( y=f\left ( X \right ) \) \( \Rightarrow \) \( R=\frac{\left [ 1+\left ( \frac{dy}{dx} \right )^{2} \right ]^{\frac{3}{2}}}{\frac{d^{2}y}{dx^{2}}} \)
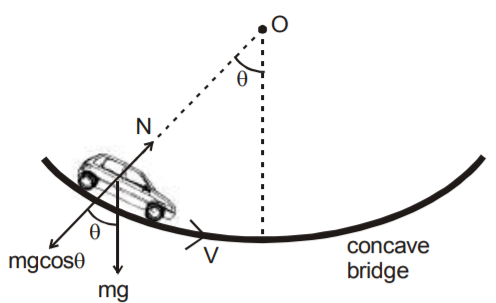
11. Normal reaction of road on a concave bridge
\( \Rightarrow \) \( N=mg \cos \Theta +\frac{mv^{2}}{r} \)
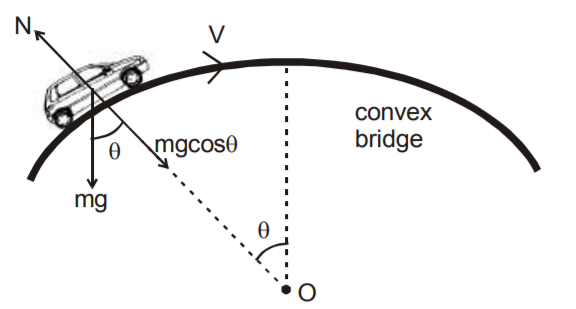
12. Normal reaction on a convex bridge
\( \Rightarrow \) \( N=mg \cos \Theta-\frac{mv^{2}}{r} \)
13. Skidding of vehicle on a level road \( \Rightarrow \) \( v_{safe}\leq \sqrt{\mu gr} \)
14. Skidding of an object on a rotating platform \( \Rightarrow \) \( \omega _{max}= \sqrt{\mu g/r} \)
15. Bending of cyclist \( \Rightarrow \) \( \tan \Theta =\frac{v^{2}}{rg} \)
16. Banking of road without friction \( \Rightarrow \)\( \tan \Theta =\frac{v^{2}}{rg} \)
17. Banking of road with friction \( \Rightarrow \) \( \frac{v^{2}}{rg}=\frac{\mu +\tan \Theta }{1-\mu \tan \Theta } \)
18. Maximum also minimum safe speed on a banked frictional road
\( v_{max}=\left [ \frac{rg\left ( \mu +\tan \Theta \right )}{\left ( 1-\mu \tan \Theta \right )} \right ]^{\frac{1}{2}} \) \( v_{min}=\left [ \frac{rg\left ( \tan \Theta -\mu \right )}{\left ( 1+\mu \tan \Theta \right )} \right ]^{\frac{1}{2}} \)
19. Centrifugal force (pseudo force) \( \Rightarrow \) \( f=m\omega ^{2} r \), acts outwards when the
particle itself is taken as a frame.
20. Effect of earths rotation on apparent weight \( \Rightarrow \) \( N=mg-mR\omega ^{2}\cos ^{2}\Theta ; \) where \( \Theta \) \( \Rightarrow \) latitude at a place
21. Various quantities for a critical condition in a vertical loop at different positions
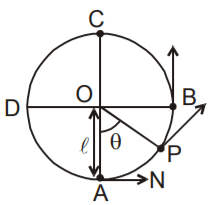

\( v_{min}=\sqrt{4gL} \) \( v_{min}=\sqrt{4gL} \) \( v_{min}=\sqrt{4gL} \) (for completing the circle) (for completing the circle) (for completing the circle)
22. Conical pendulum :
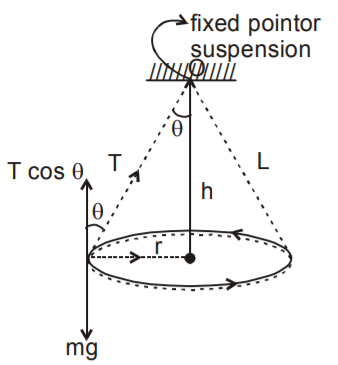
T cos \( \Theta \) = mg \( Tsin\Theta =m\omega ^{2}r \) Since Time period = \( 2\pi \sqrt{\frac{Lcos\Theta }{g}} \)
23. Relations among angular variables :
\( \omega _{0} \) \( \Rightarrow \)Initial ang. velocity \( \omega=\omega _{0}+\alpha t \)
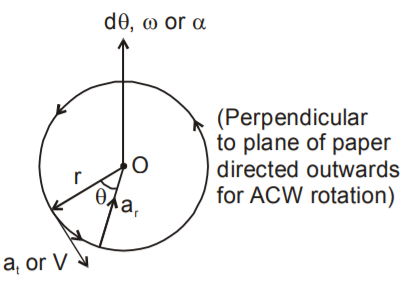
\( \omega \) \( \Rightarrow \) Find angular velocity \( \Theta =\omega _{0}t+\frac{1}{2}\alpha t^{2} \)
\( \omega \) \( \Rightarrow \) Const. angular acceleration \( \omega ^{2} =\omega _{0}^{2}+2\alpha \Theta \)
\( \Theta \) \( \Rightarrow \) Angular displacement
