“Trapezoidal Rule” is one of the important integration rules in Calculus.
In the Trapezoidal rule, the area under the curve is evaluated as trapeziums, as the total area is divided into small trapezoids instead of rectangles.
This integration is done by approximating the region under the curve of a function as a trapezoid, and the area is calculated. The Trapezoid rule formula takes the average of the left and the right sum.
Index
Formula
Let f(x) be a continuous function. The interval we will consider is [a, b].
Now dividing the intervals [a, b] into n equal subintervals, each Interval has a width of,
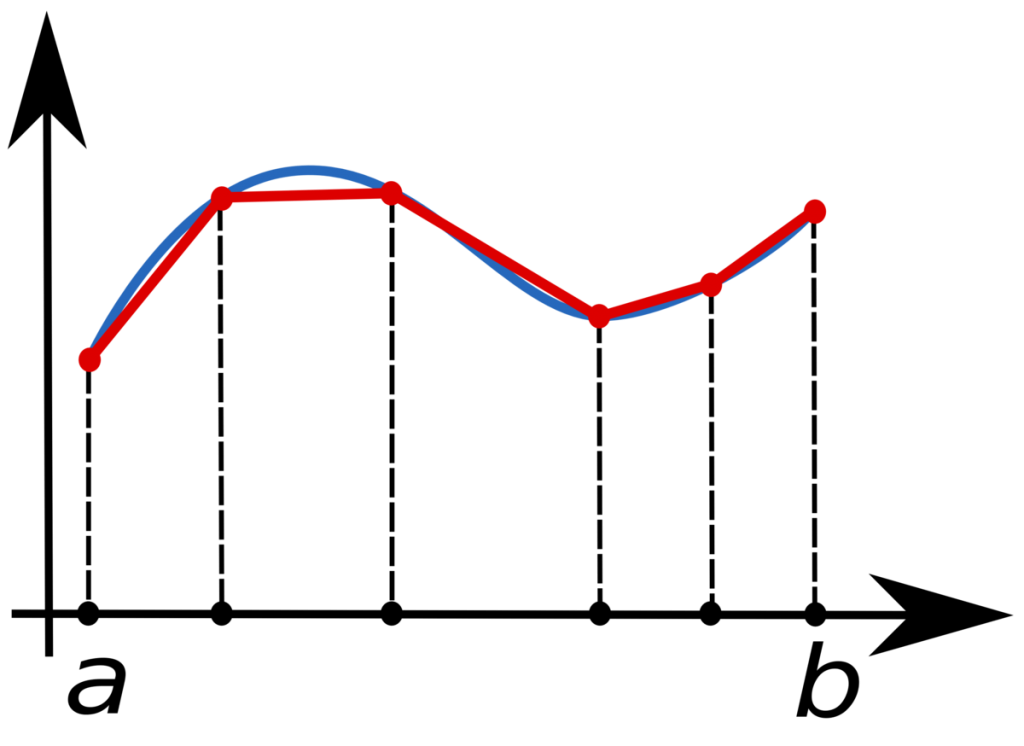
\( \Delta x = \frac{(b-a)}{n}, \) Such that \( a = x_0 < x_1< x_2<…..<x_n = b \)
Then the Trapezoidal Rule formula for area approximating integral \( \int^b_a f(x)dx \) is given by:
\( \int^b_a F(x)dx = \frac{\Delta x}{2} [ f(x_0) + 2f(x_1) + 2f(x_2) + … 2f(x_{n-1}) + f(x_n)] \)Where, \( x_i = a + i \Delta x \)
If n \( \rightarrow \infty \), R.H.S of the expression approaches the definite integral \( \int^b_a f(x)dx. \)
Trapezoidal vs Simpson’s
The Trapezoidal Rule does not provide as accurate value as Simpson’s Rule when an underlying function is smooth.
This is because Simpson’s Rule does not use linear approximations. Instead, it uses quadratic approximation. Both Simpson’s Rule and Trapezoidal Rule provide the approximation value, but Simpson’s Rule results in a more accurate approximation value of the integrals.
We can also use Riemann Sums to evaluate the definite integrals, where we use small rectangles to evaluate the area under the curve.
Related articles
Questions
Find the area under the curve which passes through the following points:
| x | 0 | 1 | 2 | 3 |
| y | 5 | 7 | 8 | 13 |
Sol. Given,
\(y_0 = 5\) \(y_1 = 7\) \(y_2 = 8\) \(y_3 = 13\) \({\Delta x} = (1 – 0) = (2 – 1) = (3 – 2) = 1\)Therefore, area = \( \frac{\Delta x}{2} [y_0 + y_n + 2(y_1 + y_2 + … + y_{n-1})] \)
=\( \frac{1}{2}[5 + 13 + 2(7 + 8)] \)
=\( \frac{1}{2} [48] \)
= 24 sq. units
Find the area under the curve \( y = 2x^2 \) through the points x = 0 to x = 3 using interval size 0.5
Sol. Given,
\( y = 2x^2 \) \( {\Delta x} = 0.5 \)| x | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 |
| y | 0 | 1 | 4 | 9 | 16 | 25 | 36 |
Area \( = \frac{0.5}{2} [0 + 36 + 2(1 +4 + 9 + 16 + 25)] \)
=\( \frac{1}{4}[146] \)
= 36.5 sq. units
FAQs
The rule is used in calculus widely. In the Trapezoidal rule, the area under the curve is evaluated as trapeziums, as the total area is divided into small trapezoids instead of rectangles.
The trapezoidal rule is used to calculate the area under a curve by dividing the area under the curve into small trapezoids. Summation of all the areas of the small trapezoids gives the area under the curve.
Area = \( \int^b_a F(x)dx = \frac{\Delta x}{2} [ f(x_0) + 2f(x_1) + 2f(x_2) + … 2f(x_{n-1}) + f(x_n)] \)
Reimann Sums uses small rectangles in order to calculate the area, while the trapezoid rule uses trapezoids.
