Factors of 96 are basically the numbers that divide it evenly or exactly without leaving any remainder i.e if a number divides 96 with a remainder of zero, then that number is called a factor.
- All Factors: 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48 and 96
- Prime Factors: 2, 3
- Factors in pairs: (1,96),(2,48),(3,32),(4,24),(6,16),(8,12)
Now, let us see the prime factors and prime factorization of the number.
Index
Prime Factorization of 96
Prime factorization is a method of “expressing” or finding the given number as the product of prime numbers. If a number occurs more than once in prime factorization, it is usually expressed in exponential form to make it more compact.
The Prime factorization here comes out to be: 2 x 2 x 2 x 2 x 2 x 3
Prime Factorization of 96 by Upside-Down Division Method
Upside-Down Division is one of the techniques of Prime factorization to find factors of any number.
In this method, you will divide a given or “composite” number evenly by the several prime numbers(starting from the smallest) till it gets a prime number.

It is called Upside-Down Division because the symbol is flipped upside down.
Here, 96 is an even number. So it is undoubtedly divisible by 2 with no remainder.
Thus we do 96÷ 2 = 48. Now find the prime factors of the obtained quotient.
Repeat Step 1 and Step 2 until we get a result of prime number as the quotient. Here, 48 is the quotient. Now find the prime factor of 48
48÷ 2 = 24
Similarly 24÷ 2 = 12
12÷ 2 = 6
Repeating the same process,
6÷2 = 3. Here, 3 is the prime number.
So we can stop the process.
So, now the prime factorization of 96 with the upside-down division method is
2 × 2 × 2 × 2 × 2 × 3.
Prime Factorization of 96 by Factor Tree Method
The Factor tree method is another technique for producing the prime factorization and all factors of a given number.
To use this method for a number x,
Firstly consider two factors say a,b of x such that a*b is equal to x and at least one of them (a, b) is a prime factor say a.
Then consider two factors of b say c, d such that again at least one of them is a prime factor. This process is repeated until both the factors are prime i.e if we get both the factors as prime at any step, we stop the process there.
Following is the factor tree of the given number.
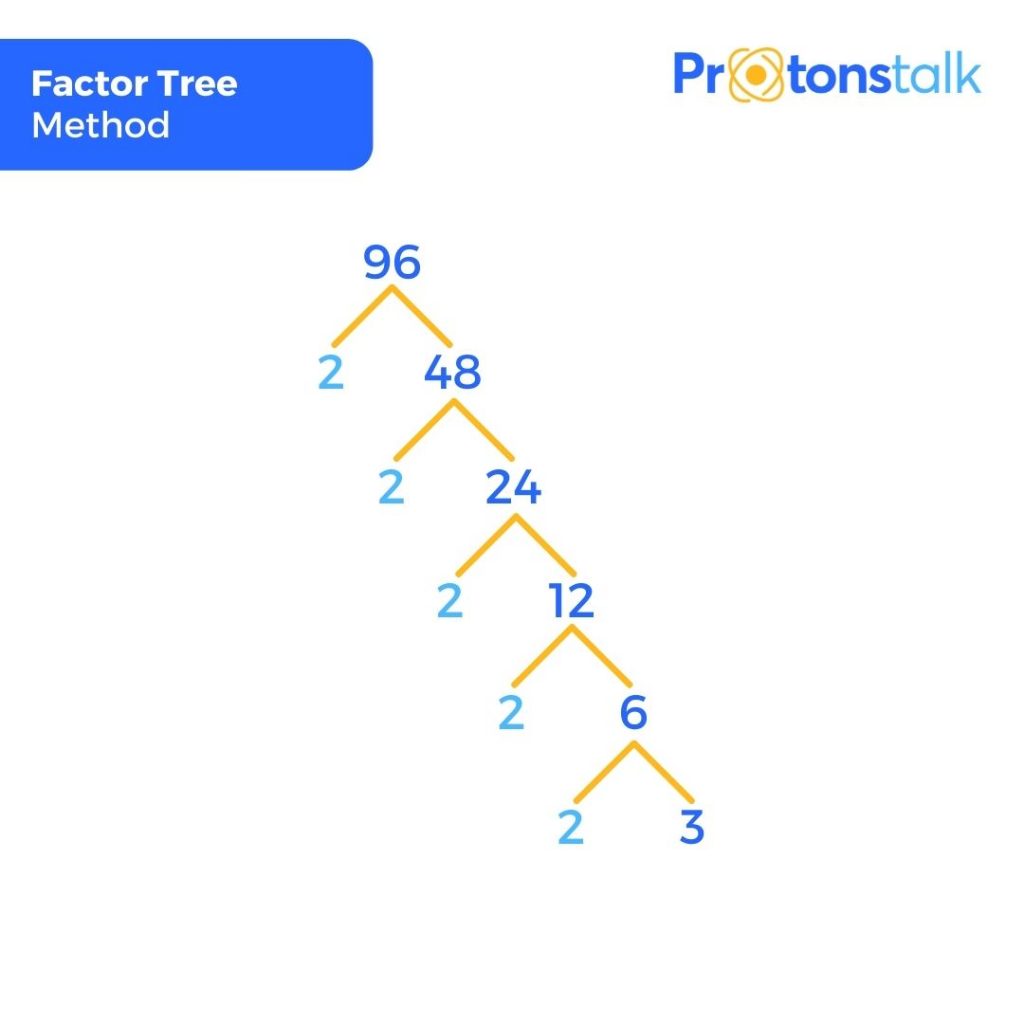
Here we can get the prime factorisation of 96 as 2 * 2 * 2 * 2 * 2 * 3 and the two prime factors are 2, 3
FAQs
Sum of all its factors = (25 + 1 – 1)/(2 – 1) × (31 + 1 – 1)/(3 – 1) = 252
The given numbers have only one common factor and that factor is 1. As a result, the Greatest Common Factor (GCF) between 96 and 19 is 1. This implies that both the given numbers are coprimes.
Factors of 96 are 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96, and the factors of 77 are 1, 7, 11, 77.
As a result, they only have one common factor: 1
More factors:
