Right Circular Cylinder

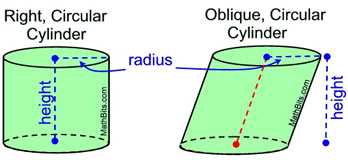
A Right Circular Cylinder is a 3-dimensional shape whose base is circular in shape. Further, the axis of the cylinder has to be perpendicular to the base for it to be a right circular cylinder. 

If the axis is not perpendicular, the circular cylinder is called an oblique circular cylinder. 

Related Terminology

Here we discuss some terms related to a circular cylinder.

1. Base: The two flat ends of a cylinder are its bases. 
2. Axis: The line joining the centers of the bases is called the axis of the cylinder.
3. Curved (lateral) Surface: It is the sides of the cylinder, which is curved. It is between the two bases.
4. Radius: It is the radius of the circular base of the cylinder.
5. Height: It is the perpendicular distance between the two bases. 

Properties of Right Circular Cylinder

A right circular cylinders have the following properties:

• Cross-sections perpendicular to the base are rectangles. In the case of an oblique circular cylinder, the same cross-section is a parallelogram.
• Cross-sections parallel to the bases are circles, both in right and oblique circular cylinders.
• In general, an oblique cross-section is an ellipse. 
• Right circular cylinders can be formed by rotating a rectangle about one of its sides. Hence, it is a solid of revolution.

Formulae for Right Circular Cylinder

Here, we discuss some important formulae related to right circular cylinders.

In all cases below, radius is denoted by \(r\), height by \(h\), and \(\pi\) is the number approximately equal to 3.14, or approximately \(\frac{22}{7}\).

Curved Surface Area

The curved or lateral surface area (CSA) is given by:

\(\text{CSA} = 2 \pi rh\)

Where,
\(r\) is radius of the base circle
\(h\) is the height of cylinder

Total Surface Area

If the cylinder is open, i.e., the bases are absent, then total surface area (TSA) is same as curved surface are (CSA). 

If the cylinder is closed, however, we have to add the areas of the bases. So we get,

\(
\begin{align}
\text{TSA} & = \text{CSA} + \text{base area} \\
& = 2 \pi rh + 2\cdot \pi r^2 h \\
& = 2 \pi r (r+h)
\end{align}
\)

Volume of Right Circular Cylinder

For any cylinder, the volume is given by the product of base area and height. So, the volume of right circular cylinder is given as follows:

\(
\begin{align}
\text{Volume (V)} & = \text{Base area} \times \text{Height} \\
& = \pi r^2 \times h \\
& = \pi r^2 h
\end{align}
\)

Solved Examples

Question 1. Find the curved and total surface area of right circular cylinders having radius as 7 cm and height as 10 cm.

Solution. We know that,
\(\text{CSA} = 2\pi rh\) and \(\text{TSA} = 2\pi r(h+r)\).

So we have,

\(
\begin{align}
\text{CSA} & = 2 \pi rh \\
& =2 \times \frac{22}{7} \times 7 \times 10 \\
& = 440 {\text{ cm}}^2
\end{align}
\)

\(
\begin{align}
\text{TSA} & = 2 \pi r(h+r) \\
& =2 \times \frac{22}{7} \times 7 \times (10+7) \\
& = 748 {\text{ cm}}^2
\end{align}
\)

Thus, the curved surface area of this cylinder is 440 sq. cm, and the total surface area is 748 sq. cm.

Question 2. The volume of right circular cylinder is 4400 cubic cm. If its height is 14 cm, what is its base radius?

Solution. We know that, for right circular cylinders,
\(\text{Volume (V)}= \pi r^2 h\)

Solving this equation, we have,

\(
\begin{align}
4400 & = \pi r^2 h \\
& = \frac{22}{7} \times r^2 \times 14 \\
\end{align} \\
\Rightarrow 4400 = 44 \times r^2 \\
\Rightarrow 100 = r^2 \\
\Rightarrow r = 10 \text{ cm} \\
\)

Thus, the radius is 10 cm. 

FAQs