Projectile Motion is the form of motion observed when any object is launched into the air. The Projectile motion is subjected to only acceleration due to gravity. The object launched is called Projectile and its path is called Trajectory.
Formulas
The formulas related to Projectile Motion are as follows :
Time of flight : T = \( \frac{2u \sin \theta}{g} \)
Horizontal range : R = \( \frac{u^{2} \sin 2\theta}{g} \)
Maximum height : H = = \( \frac{u^{2} \sin^{2} \theta}{2g} \)
Trajectory equation (equation of path) : y = x tan \( \theta – \frac{gx^{2}}{2u^{2}\cos^{2}\theta} \Rightarrow x \tan \theta \left ( 1-\frac{x}{R} \right ) \)
Projection on an inclined plane
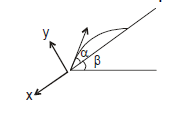
| Up the incline | Down the incline | |
| Range | \(\frac{2 u^{2}sin\alpha cos(\alpha + \beta)}{g cos^{2} \beta}\) | \(\frac{2 u^{2}sin\alpha cos(\alpha – \beta)}{g cos^{2} \beta}\) |
| Time of flight | \(\frac{2 u sin\alpha}{g cos \beta}\) | \(\frac{2 u sin\alpha}{g cos \beta}\) |
| The angle of projection with an inclined plane for maximum range | \(\frac{\pi}{4} – \frac{\beta}{2}\) | \(\frac{\pi}{4} + \frac{\beta}{2}\) |
| Maximum range | \(\frac{u^{2}}{g(1+sin \beta)}\) | \(\frac{u^{2}}{g(1-sin \beta)}\) |
